|
Cubique
° Nombre cubique. –
Nombre figuré qui est engendré par un
cube. Les nombres cubiques de dimensions 2, 3, 4 et 5 sont définis.
n Nombre gnomonique
cubique ou cubique D2
Nombre plan ou de dimension 2 qui est représenté par
le gnomon
d’un cube. Tout nombre de cette classe est la différence de deux cubiques D3
successifs. Le terme général de rang n est (3n2
- 3n + 1). Les dix plus petits gnomoniques cubiques sont : 1, 7, 19,
37, 61, 91, 127, 169, 217 et 271. La suite des gnomoniques cubiques est
la même que celle des centrés hexagonaux
D2et celle des centrés étoilés
triangulaires.
n Nombre cubique
ou cubique D3
Nombre polyédrique
de dimension 3 qui est engendré par un cube. Tout nombre de rang n de
cette classe est la somme des n premiers gnomoniques
cubiques. Le terme
général est n3. Les quatre plus petits
nombres cubiques peuvent être représentés ainsi :
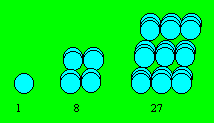
La différence des carrés de deux triangulaires
successifs
est un cubique. Le rang du cubique D3 est le rang du plus grand triangulaire. Pour
trouver son successeur, on élève au cube le rang suivant ou encore on lui
additionne le triple du produit des deux rangs plus 1. Par exemple,
2197 est cubique car 912 - 782
= 2197. Les nombres 78 et 91 sont les triangulaires de rangs 12 et 13. Aussi,
2197 est au rang 13. Son successeur est 143 =
2197 + (3 × 13 × 14 + 1) = 2744. Les 49 plus petits cubiques D3 sont :
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
|
1 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
729 |
|
1 |
1000 |
1331 |
1728 |
2197 |
2744 |
3375 |
4096 |
4913 |
5832 |
6859 |
|
2 |
8000 |
9261 |
10 648 |
12 167 |
13 824 |
15 625 |
17 576 |
19 683 |
21 952 |
24 389 |
|
3 |
27 000 |
29 791 |
32 768 |
35 937 |
39 304 |
42 875 |
46 656 |
50 653 |
54 872 |
59 319 |
|
4 |
64 000 |
68 921 |
74 088 |
79 507 |
85 184 |
91 125 |
97 336 |
103 823 |
110 592 |
117 649 |
Voici quelques
propriétés concernant les nombres de cette classe :
La période des unités des nombres successifs correspond à un nombre de 10
chiffres différents : 1 874 563 290.
Les cubes des entiers dont l'unité est 0, 1, 4, 5, 6 ou 9 sont terminés
respectivement par ces mêmes chiffres ; les cubes des entiers terminés par 2,
3, 7 et 8 sont respectivement terminés par 8, 7, 3 et 2.
La somme des n premiers cubiques D3 est un hypercubique
de rang n.
La différence de deux cubiques D3 successifs est un centré hexagonal
D2.
Le gnomon d'un cubique D3 est un centré hexagonal D2.
Tout cubique D3 est la différence de deux hypercubiques successifs.
Tout cubique n3 est la somme des n
impairs successifs commençant avec [n(n - 1) + 1].
Tout cubique est soit un multiple de 9, soit un multiple de 9 augmenté ou
diminué de l'unité.
La somme des cubes des n plus petits entiers est le carré de la somme
des n plus petits entiers. Elle est égale à (1 + 2 + 3 + ... + n)2.
La somme d’au moins trois cubes peut être un cube. Exemples : 33
+ 43 + 53 = 63
et 63 + 83 +
103 = 123.
L’ensemble des cubiques D3 forme une suite arithmétique de degré 3.
La suite des cubiques est la même que celle des centrés
hexagonaux D3. Dans sa forme
arithmétique, un nombre cubique D3 est appelé cube parfait.
n Nombre hypercubique
ou cubique D4
Nombre polyédrique de dimension 4 qui est engendré par un cube. Tout nombre de
rang n de cette classe est la somme des n premiers cubiques. Le
terme général est n2(n + 1)2/4.
Les 29 plus petits hypercubiques sont :
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
|
1 |
9 |
36 |
100 |
225 |
441 |
784 |
1296 |
2025 |
|
1 |
3025 |
4356 |
6084 |
8281 |
11 025 |
14 400 |
18 496 |
23 409 |
29 241 |
36 100 |
|
2 |
44 100 |
53 361 |
64 009 |
76 176 |
90 000 |
105 625 |
123 201 |
142 884 |
164 836 |
189 225 |
Un nombre est hypercubique si sa racine carrée est un triangulaire. Son rang est celui du triangulaire. Pour trouver son successeur,
on élève au carré le triangulaire de rang suivant. Par exemple, 784 est un
hypercubique car il est le carré de 28 qui est le triangulaire de rang 7. Son
successeur est 362 = 1296.
Voici quelques
propriétés concernant les nombres de cette classe :
La période des unités des nombres successifs correspond à un palindrome de 20
chiffres : 01 960 514 655 641 506 910.
Les unités sont 0, 1, 4, 5, 6 et 9.
La différence de deux hypercubiques successifs est un cubique.
Tout hypercubique est la différence de deux cubiques D5 successifs.
L’ensemble des hypercubiques forme une suite arithmétique de degré 4.
La suite des hypercubiques est la même que celle des centrés
hexagonaux D4.
n Nombre cubique
D5
Nombre polyédrique de dimension 5 qui est engendré par un cube. Tout nombre de
rang n de cette classe est la somme des n premiers hypercubiques.
Le terme général est n(n + 1)(n + 2)(3n2
+ 6n + 1)/60. Les 10 plus petits cubiques D5 sont : 1, 10, 46, 146,
371, 812, 1596, 2892, 4917 et 7942. Les différences successives des suites à
partir de la suite des cubiques D5 sont :

La suite des cubiques D5 est la même que celle des centrés
hexagonaux D5.
© Charles-É.
Jean
Index
: C
|
![]()
![]()