Dictionnaire de mathématiques récréatives Nombre gnomonique

Gnomonique

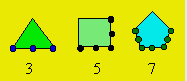
° Nombre gnomonique. – Nombre linéaire ou de dimension 1 qui est représenté par le gnomon d'un polygone régulier. Les gnomons d’un triangle, d’un carré et d’un pentagone peuvent être illustrés ainsi :

Voici un tableau donnant les 10 plus petits nombres de huit classes de gnomoniques :

Classe/Rang n	1	2	3	4	5	6	7	8	9	10	Terme général
Triangulaire	1	2	3	4	5	6	7	8	9	10	n
Carré	1	3	5	7	9	11	13	15	17	19	2n - 1
Pentagonal	1	4	7	10	13	16	19	22	25	28	3n - 2
Hexagonal	1	5	9	13	17	21	25	29	33	37	4n - 3
Heptagonal	1	6	11	16	21	26	31	36	41	46	5n - 4
Octogonal	1	7	13	19	25	31	37	43	49	55	6n - 5
Ennéagonal	1	8	15	22	29	36	43	50	57	64	7n - 6
Décagonal	1	9	17	25	33	41	49	57	65	73	8n - 7
Raison	1	1	2	3	4	5	6	7	8	9	n - 1

Le terme général de rang n d'un polygone de k côtés est (k - 2)n - (k - 3). Tout gnomonique d'un polygone de k côtés à partir de k = 3, auquel on additionne (k - 3) est un multiple de (k - 2).

L’ensemble des gnomoniques forme une suite arithmétique de degré 1. Les gnomoniques sont des nombres figurés.

Index : G