|
| |
|

|
Publications |
|
Ceci est le septième livre édité par Récréomath.
Au jeu
Par Charles-É. Jean
|
* * *
* * * * * * *
Solutions
|
Chapitre 1.
Récréations arithmétiques
1. Plus ou moins
Une expression est : 1 - 23 - 4 + 56 - 7.
2. Quatre groupes
La somme des nombres de 1 à 16 est 136. La somme des nombres de chaque
groupe est donc 34. Voici quatre groupes possibles :
1, 2, 15, 16
3, 4, 13, 14
5, 6, 11, 12
7, 8, 9, 10
3. Chiffres uniques
Voici une égalité : 79 + 48 + 26 = 153. Il existe 54 égalités. Les
sommes possibles sont : 153 (6 sommes), 162 (6 sommes), 189 (6 sommes), 216 (18
sommes), 234 (12 sommes) et 243 (6 sommes).
4. Nombres de trois chiffres
Les nombres sont 357, 492 et 816.
5. Des timbres cachés
On peut établir le diagramme suivant en
choisissant deux variables a et b.
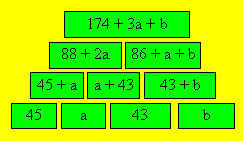
À partir du tableau, on forme deux
équations.
(1) 174 + 3a + b = 347.
D'où 3a + b = 173
Par ailleurs, comme le nombre total de
timbres est 1136, on peut écrire :
(2) 567 + 9a + 4b =
1136. D'où 9a + 4b = 569.
En résolvant les deux équations, on
obtient : a = 41 et b = 50. Le tableau ci-dessous indique le
nombre de timbres dans chaque case.
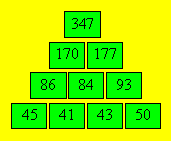
6. Une somme
On peut former 24 nombres. Chaque colonne
(unité, dizaine, centaine, unité de mille) est composée de six 1, six 2, six
3 et six 4. La somme des nombres de chaque colonne est 60.
La somme totale est 66 660.
7. En progression
Les grilles remplies sont :
|
3 |
7 |
11 |
15 |
|
2 |
7 |
12 |
17 |
|
5 |
10 |
15 |
20 |
|
8 |
12 |
16 |
20 |
|
7 |
13 |
19 |
25 |
|
14 |
17 |
20 |
23 |
|
9 |
16 |
23 |
30 |
|
20 |
22 |
24 |
26 |
8.
Un cycle
On écrit toutes les sommes pour obtenir quatre
équations :
(1) x + y
+ z = 10
(2) y + z
+ t = 11
(3) z + t
+ x = 6
(4) t + x + y
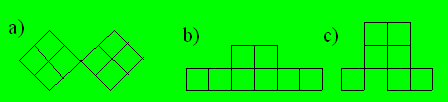
= 12
Soustrayons
quelques équations :
(4) - (1) : t
- z = 2
(4) - (2) : x
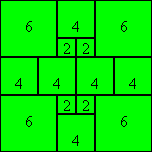
- z = 1
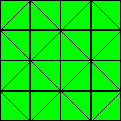
(4) - (3) : y
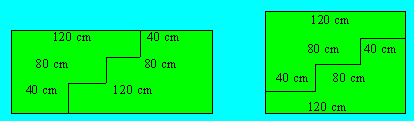
- z = 6
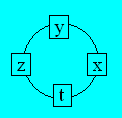
Si on fait la somme des trois dernières équations, on
obtient : t + x + y - 3z = 9.
D'où, z est égal à 1.
Si z = 1, alors t = 3, x
= 2 et y = 7.
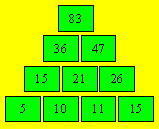
9. Pyramides de nombres
a) Voici cinq pyramides :
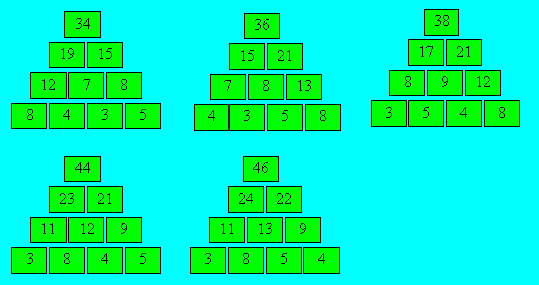
b) La pyramide a le plus petit sommet
quand les deux cases centrales de la rangée inférieure contiennent les plus
petits nombres, 6 et 7. Le sommet est alors 56. Elle a le plus grand sommet
quand ces cases contiennent les deux plus grands nombres, 8 et 9.
Le sommet est alors 64.
c) Il existe 12 pyramides différentes.
d) La case centrale de la rangée
inférieure contient 15. Il s'agit alors de choisir deux nombres dont la somme
est 33 pour les deux autres cases.
e) Les deux cases centrales de la
rangée inférieure contiennent deux nombres dont la somme est 8. Les deux
autres cases ont une somme de 112.
f) Voici la pyramide complétée :
10. L'intersection
Voici comment on peut distribuer les
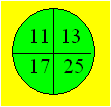
nombres dans le tableau :
|
15 |
21 |
12 |
|
10 |
19 |
7 |
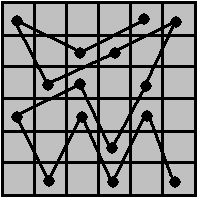
|
40 |
22 |
16 |
11. Numéros de rues
Les deux amis
demeurent respectivement sur la 19e et sur la
31e rue.
12. Divisibilité par 7
Voici trois nombres qui satisfont aux
propriétés : 123 456 879, 123 457 698 et 123 458 769.
13. Vers le million
Le plus grand nombre est donné en fonction de
chaque diviseur de 2 à 19.
|
2 |
999 998 |
11 |
999 999 |
|
3 |
999 999 |
12 |
999 996 |
|
4 |
999 996 |
13 |
999 999 |
|
5 |
999 995 |
14 |
999 992 |
|
6 |
999 996 |
15 |
999 990 |
|
7 |
999 999 |
16 |
999 984 |
|
8 |
999 992 |
17 |
999 991 |
|
9 |
999 999 |
18 |
999 990 |
|
10 |
999 990 |
19 |
999 989 |
14.
En cercles
On écrit les quatre
équations.
(1) xyz =
60 (2) yzt
= 70 (3) ztx =
84 (4) txy =
210
On divise la première équation par chacune des trois autres.
(1) ÷ (2) : x/t
= 6/7
(1) ÷ (3) : y/t
= 5/7
(1) ÷ (4) : z/t
= 2/7

On obtient : t = 7, x = 6,
y = 5 et z = 2.
15.
L'avoir de Nathalie
Les multiples de 6 inférieurs à 59 sont : 6,
12, 18, 24, 30, 36, 42, 48, 54.
Si
le reste est 5, les montants possibles sont : 11, 17, 23, 29, 35, 41, 47, 53.
Les
multiples de 5 inférieurs à 59 sont : 5, 10, 15, 20, 25, 30, 35, 40, 45, 50,
55.
Si
le reste est 4, les montants possibles sont : 9, 14, 19, 24, 29, 34, 39, 44, 49,
54.
Seul
29 apparaît à la fois dans les suites de la deuxième et de la quatrième
ligne.
Nathalie possède 29 $.
16. Montants doubles
Jules a 215 $. Judith a 430 $.
17. Une table de multiplication
Il manque les nombres premiers supérieurs à 12
et inférieurs à 144. Ce sont : 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,
61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137,
139.
Il manque 29 nombres.
18. Itinéraire
La chaîne d’opérations est : + 8, - 1,
+ 6, - 10, × 7, ÷ 5, + 3, - 11, + 4, - 9, × 2.
19. Les jeans d'Éric
Soit A : Axès, B : Bexès, C : Cexès, D :
Dexès
On aura l'équation A2
+ B2 = C2 + D2.
En supposant des valeurs aux variables tout en tenant compte du dernier chiffre
de la somme de chaque paire, on obtient 242 +
412 = 362 + 312.
Éric a vendu 24 paires de jeans Axès,
41 Bexès, 36 Cexès et 31 Dexès.
20. Un mois de novembre
On part du jour donné. On cherche le jour de la
semaine correspondant au 1er novembre 2014, c'est un samedi. Il y a,
entre le même jour de deux années consécutives, un décalage d'un jour de la
semaine sauf deux jours à la suite d'une année bissextile.
Entre 2006 et 2014, le 1er
novembre qui tombe un dimanche est en 2009.
21.
Avec 1982
Les quatre égalités sont :
(1 + 9 - 8) ÷ 2
= 1
(1 + 9 + 8) ÷ 2
= 9
1 - 9 + 8 × 2 =
8
1 - 9 + 8 + 2 = 2
22. Beaucoup de 7
Il y a 12 nombres : 637, 1267, 1897, 2527, 3157,
3787, 4417, 5047, 5677, 6307, 6937 et 7567.
23. Une astuce de calcul
Les coûts totaux du couteau, des poêles, des
bols et des moules sont respectivement divisibles par 3. Le montant total
devrait donc être divisible par 3 : ce qui n'est pas le cas.
24. Des cases vides
|
36 |
est le carré de |
6 |
|
16 |
est le nombre qui suit |
15 |
|
20 |
est le double de |
10 |
|
25 |
est inférieur de 10 à |
35 |
|
12 |
est le renversé de |
21 |
|
54 |
est le triple de |
18 |
Le nombre qui reste est 75.
25. Chemin d'opérations
Le chemin est donné dans ce tableau.
26. L'âge de Sextus
Le problème posé pourrait se traduire ainsi :
Le nombre 12 243 est en base 6. Transformez-le en base 10.
On peut écrire : (1 × 64)
+ (2 × 63) + (2 × 62)
+ (4 × 61) + (3 × 60)
= 1827.
Sextus a 1827 ans.
27. Pair et impair
Il s'agit de trouver entre 50 et 90 un nombre
pair dont la somme des chiffres est 15. Ce nombre est 78.
28. Mur de briques
Le chiffre de la case supérieure est
nécessairement 1, car la somme des huit nombres est 12 068. Le chiffre de
gauche de la seconde rangée supérieure est 1 ou 8 car 1190 et 1890 sont
divisibles par 7. À cause de la somme totale, il faut rejeter 8. Les nombres
sont : 1120, 1127, 1197, 1190, 1897, 1890, 1820 et 1827.
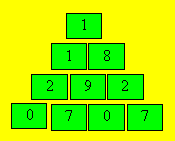
29. Commerce de légumes
Une stratégie consiste à supposer un montant
de départ, disons 10 000 $, pour l'avoir de Romain. À chaque tranche de trois
ans, son avoir augmente de 1000 $. À la fin de la 33e année, il aurait 21 000
$ et à la fin de la 35e année 22 200 $. Or, son avoir réel est de 20 000 $.
Le montant hypothétique dépasse le montant réel de 2200 $. On retranche ce
montant de 10 000 $.
L'avoir de Romain est de 7800 $.
30. À la renverse
Les nombres sont 34 et 43.
31.
Vers 25
Cinq 2 : 22 + 2 + 2/2 ou (2 + 2 + 2/2)2
Cinq
3 : 33 - (3 + 3)/3
Six
4 : 4 × 4 + 4 + 4 + 4/4
Quatre
5 : 5 × 5 + 5 - 5 ou 5 × 5 × 5/5
32. Tiers et quarts
Le nombre est 264.
33. Anniversaires
Émilie a fêté 17 anniversaires de naissance.
L'année 1900 n'était pas bissextile.
34.
Faites votre choix
a) Vrai, car n + (n + 1) + (n
+ 2) + ... + (n + 18) = 19n + 171.
b)
Faux, car le dernier chiffre est 6.
c)
Vrai, car 7 × 11 × 13 = 1001.
35.
D'un à l'autre
a) × 3, - 3, ÷ 2, - 5
b)
- 3, × 2, + 6, ÷ 2
c)
÷ 2, + 4, + 6, × 2, × 3, - 3, - 5. Ce qui donne 82.
36.
Des oeufs
a) 72 oeufs - 1 oeuf ou 71 oeufs coûtent 5,68
$.
Un
oeuf coûte 8 ¢.
Une
douzaine d'oeufs de classe A coûte 96 ¢.
b)
144 oeufs - 6 oeufs ou 138 oeufs coûtent 10,35 $.
Un
oeuf coûte 7,5 ¢.
Une
douzaine d'oeufs de classe B coûte 90 ¢.
37. Dissections
Soit x le nombre cherché. Ce nombre est
égal à (x/7 - 63) (x/14 - 35) (x/21 - 24). Il est donc
divisible par 42. À cause de cela, il est supérieur à 21 × 24 ou 504.
Le nombre cherché est 588.
38.
Avec 1985
Voici deux expressions pour chaque cas :
3 :
(15 + 9)/8 ou (9 × 1) / (8 - 5)
6
: (1 + 8)/9 + 5 ou 9 × 1 - 8 + 5
12
: (95 + 1)/8 ou 8 - 5 + 9 × 1
18
: (89 + 1)/5 ou 9(8 - 5 - 1)
39. En paires
Les couples sont successivement (18, 26), (11,
16) et (7, 28). Le nombre qui reste est 32.
40.
Avec 1978
Une façon de distribuer les chiffres et les
opérations est donnée dans chaque cas.
40 : (8 - 1)7 -
9 41 : 8Ö9
+ 17
42 : 7(Ö9 + Ö1+8)
43 : 17 × Ö9
- 8 44 : (7 + 8)Ö9
- 1 45 : (7 + 8)Ö9
× 1
46 : 7 × 8 - 1 -
9 47 : (7 × 8 - 9)1
48 : (7 × 8) + 1 - 9
49 : (8 - 1)9-7
41.
Avec 1986
Une façon de distribuer les chiffres et les
opérations est donnée dans chaque cas.
1 : 8 + 9 - 16
2 : 6 + Ö9 - 8 + 1
3 : (9 + 8 + 1)/6
4 : 6 + 8 - 9 - 1
5 : 19 - 8 - 6
6 : 9 + 6 - 8 - 1
7 : 9 - 8 + 6 ×
1 8 : 6 + 18/9
9 : 18/6 × Ö9
10 : 9 + 8 - 6 - 1
42. Divisibilité par 5
Le dernier chiffre de la 20e
puissance de 2 est 6 et celui de 3 est 1. Par ailleurs, on sait qu'un nombre est
divisible par 5 quand il se termine par 0 ou 5.
a) non
b) oui c) non
d) non
43. Extractions
La racine quatrième de 1000 est 5,62 ; celle de
10 000 est 10. La base est entre 5 et 10. Seul 8 satisfait les conditions
puisque c'est un cube. Un seul nombre existe : 4096.
44. Dernier chiffre
a) Les puissances de 2 sont 2, 4, 8, 16, 32, 64,
128, etc. Le dernier chiffre est successivement 2, 4, 8, 6 de façon
périodique. En divisant 57 par 4, on obtient 14 reste 1. Donc, le dernier
chiffre de 257 est le même que celui de 21
soit 2.
b) Le dernier chiffre est 6.
c) Le dernier chiffre est 1.
45. Nombres croisés
On cherche d'abord la valeur de a. À
cause de l'indice A, a est un entier entre 31 et 100. À cause de
l'indice F, a est inférieur à 92. À cause de l'indice G, la case (G,
C) contient 0 et la case (G, D) contient 3. En continuant les vérifications, on
obtient : a = 83 et b = 51. La grille remplie est :
|
|
E |
F |
G |
H |
|
A |
6 |
8 |
8 |
9 |
|
B |
4 |
2 |
3 |
3 |
|
C |
7 |
8 |
0 |
2 |
|
D |
4 |
1 |
3 |
2 |
46. Tout en carré
Il existe une infinité de cas où l'égalité
se vérifie. Il s'agit de la règle d'Hoppenot qui pourrait s'énoncer ainsi :
La somme des carrés de n entiers consécutifs où le plus grand est 2n(n
- 1) est égale à la somme des carrés des (n - 1) entiers consécutifs
suivants. Voici des exemples :
32
+ 42 = 52
102
+ 112 + 122 =
132 + 142
212
+ 222 + 232 +
242 = 252 + 262
+ 272
362
+ 372 + 382 +
392 + 402 = 412
+ 422 + 432 +
442
47.
Au hasard
Il peut exister plusieurs égalités. En voici
une pour chaque cas :
a) 21 × 5 - 17 × 4
- 22 = 15
b) 7 × 8/4 - 22/2 =
3
c) Ö3×27
+ (12 × 8)/16 = 15
d) (12 + 7 - 10 - 6) ¸
3 = 1
48. Une charade
Mon premier a deux chiffres : 16, 25, 36, 49, 64
ou 81.
Mon second a un chiffre : 1, 4 ou 9.
Mon tout est 169 ou 361.
|
|
|
Chapitre 2. Récréations
combinatoires
49. Un carré incomplet
Le terme du milieu
d'un carré magique d'ordre 3 est égal au tiers de la densité c’est-à-dire
de la somme de chaque rangée horizontale, verticale et diagonale. La densité
étant 42, on peut placer 7 et 15. Puis, comme la somme des deux termes d'une
oblique est le double du terme du coin opposé, on place 18, 17, 11 et 10. Voici
le carré magique :
|
18 |
7 |
17 |
|
13 |
14 |
15 |
|
11 |
21 |
10 |
50. Magie alternative
Voici une disposition des nombres :
51. Carrés premiers
Voici deux carrés magiques :
|
101 |
29 |
83 |
|
277 |
31 |
163 |
|
53 |
71 |
89 |
|
43 |
157 |
271 |
|
59 |
113 |
41 |
|
151 |
283 |
37 |
52. Octomagie
Voici un carré magique :
|
8 |
2 |
3 |
5 |
|
5 |
3 |
2 |
8 |
|
1 |
7 |
6 |
4 |
|
4 |
6 |
7 |
1 |
53. La magie de 1982
Voici deux façons de
distribuer les nombres :
|
1 |
9 |
8 |
2 |
|
1 |
9 |
8 |
2 |
|
9 |
2 |
1 |
8 |
|
9 |
8 |
2 |
1 |
|
8 |
1 |
2 |
9 |
|
8 |
2 |
1 |
9 |
|
2 |
8 |
9 |
1 |
|
2 |
1 |
9 |
8 |
54. Vingt-cinq cases
Voici les deux carrés :
|
11 |
18 |
25 |
2 |
9 |
|
15 |
24 |
1 |
8 |
17 |
|
23 |
5 |
7 |
14 |
16 |
|
3 |
12 |
19 |
21 |
10 |
|
4 |
6 |
13 |
20 |
22 |
|
22 |
6 |
13 |
20 |
4 |
|
10 |
12 |
19 |
21 |
3 |
|
16 |
5 |
7 |
14 |
23 |
|
17 |
24 |
1 |
8 |
15 |
|
9 |
18 |
25 |
2 |
11 |
55. Déplacements
On dispose 9 à la
place de 11 et réciproquement ; 5 à la place de 7 et réciproquement ; 12 à
la place de 10 et réciproquement.
56. Quarante-neuf cases
Après avoir placé 4 dans la case centrale de
la première ligne, on avance à droite vers le haut. Lorsque la case est en
dehors du carré, on prend la case vis-à-vis. Si la case est déjà remplie, on
continue dans la case placée sous celle-ci. Voici le carré rempli :
|
33 |
42 |
51 |
4 |
13 |
22 |
31 |
|
41 |
50 |
10 |
12 |
21 |
30 |
32 |
|
49 |
9 |
11 |
20 |
29 |
38 |
40 |
|
8 |
17 |
19 |
28 |
37 |
39 |
48 |
|
16 |
18 |
27 |
36 |
45 |
47 |
7 |
|
24 |
26 |
35 |
44 |
46 |
6 |
15 |
|
25 |
34 |
43 |
52 |
5 |
14 |
23 |
57. Soixante-quatre cases
Ce carré semi-magique
a été inventé par Leonhard Euler, un mathématicien suisse du 18e siècle.
|
1 |
48 |
31 |
50 |
33 |
16 |
63 |
18 |
|
30 |
51 |
46 |
3 |
62 |
19 |
14 |
35 |
|
47 |
2 |
49 |
32 |
15 |
34 |
17 |
64 |
|
52 |
29 |
4 |
45 |
20 |
61 |
36 |
13 |
|
5 |
44 |
25 |
56 |
9 |
40 |
21 |
60 |
|
28 |
53 |
8 |
41 |
24 |
57 |
12 |
37 |
|
43 |
6 |
55 |
26 |
39 |
10 |
59 |
22 |
|
54 |
27 |
42 |
7 |
58 |
23 |
38 |
11 |
58. Un rapport incomplet
Voici le rapport complet :
|
|
1er trimestre |
2e trimestre |
3e trimestre |
|
Mélanie |
83 |
60 |
76 |
|
Julie |
66 |
73 |
80 |
|
Pierre-Luc |
70 |
86 |
63 |
59. Des théorèmes
a) On peut démontrer la proposition ainsi. Soit
le carré :
|
a1 |
a2 |
a3 |
|
a4 |
a5 |
a6 |
|
a7 |
a8 |
a9 |
Soit D la densité. On peut alors écrire :
a1
+ a5 + a9 = D
a2
+ a5 + a8 = D
a3
+ a5 + a7 = D
a4
+ a5 + a6 = D
On additionne les quatre équations et on obtient :
a1
+ a2 + a3 + a4
+ 4a5 + a6 + a7
+ a8 + a9 = 4D
(a1
+ a2 + a3) +
(a4 + a5 + a6)
+ (a7 + a8 + a9)
+ 3a5 = 4D
D
+ D + D + 3a5 = 4D
3a5
= D
a5
= D/3
D'où, le terme du milieu est toujours
le tiers de la densité du carré magique d'ordre 3.
b) On place la variable k au
centre d'un carré magique. On ajoute et retranche a sur la diagonale de
gauche, puis b sur la diagonale de droite. On complète les autres cases
de façon à obtenir 3k comme densité. Le carré suivant est bien
magique.
|
k + a |
k - a - b |
k + b |
|
k - a + b |
k |
k + a - b |
|
k - b |
k + a + b |
k - a |
Il nous reste à vérifier l'égalité
des sommes des carrés respectivement de la première ligne et de la troisième
ligne.
(k + a)2
+ (k - a - b)2 + (k
+ b)2 = (k - b)2
+ (k + a + b)2 + (k
- a)2 = 3k2
+ 2a2 + 2ab + 2b2
c) Dans un carré magique d'ordre 3, la
somme des carrés des éléments de la première rangée verticale est égale à
la somme des carrés des éléments de la troisième rangée verticale.
La démonstration de cette proposition
se fait de la même façon que précédemment. En prenant le même carré
magique, on aura :
(k + a)2
+ (k - a + b)2 + (k
- b)2 = (k + b)2
+ (k + a - b)2 + (k
- a)2 = 3k2
+ 2a2 - 2ab + 2b2
60. Un système d'équations
Ce problème est une application d'un théorème
sur les carrés magiques qui s'énonce comme suit. Dans un carré magique
d'ordre 3, la somme des carrés des éléments de la première rangée
horizontale est égale à la somme des carrés des éléments de la troisième
rangée horizontale.
On place 5, 12 et 13 sur la première
ligne. La densité du carré magique est 30. Comme dans un carré magique, le
terme du milieu est toujours le tiers de la densité du carré magique. Ce terme
est égal à 10 : ce qui nous permet de compléter le carré magique.
Les valeurs de d, e et f
sont respectivement 7, 8 et 15. Ces nombres apparaissent sur la troisième ligne
du carré magique.
61. Un triangle dense
On attribue une lettre à chaque case.
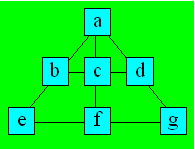
Soit
s la somme des nombres de chaque rangée et S la somme totale des
nombres. On aura :
a
+ e = c + d, car a + b + e = b
+ c + d
a
+ f = b + d, car a + c + f = b
+ c + d
a
+ g = b + c, car a + d + g = b
+ c + d
En
additionnant membre à membre ces trois équations, on obtient :
3a
+ e + f + g = 2b + 2c + 2d
3a
+ s = 2s
D'où,
3a = s.
Comme la somme s des nombres de
chaque rangée est 18, alors a est égal à 6. D'où, b + e
= c + f = d + g = 12. On a donc trois groupes : (1,
11), (2, 10) et (5, 7). Les nombres peuvent être disposés ainsi :
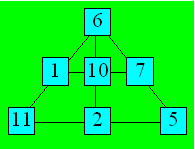
62. Un autre triangle dense
La somme totale des nombres est 70. La case du
haut contient 10. La distribution des nombres peut se faire ainsi :
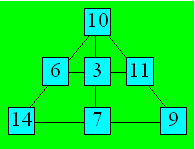
63. Un triangle quadruplé
Voici les quatre façons de distribuer les
nombres :

64. Distractions
a) On attribue une lettre à chaque case.
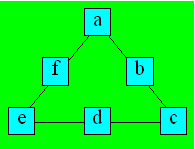
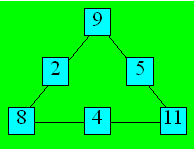
On peut montrer que c + f
= b + e = a + d. La somme de tous les nombres
donnés est 39. On partage ces nombres en trois groupes de somme égale : (2,
11), (4, 9) et (5, 8). Chaque groupe contient un sommet et le terme du milieu du
côté opposé à ce sommet. Une disposition des nombres est :
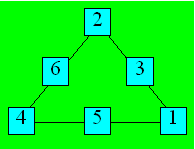
b) Voici une façon de distribuer les nombres :
c) Le plus grand résultat sur chaque côté est 8.
Voici une façon de distribuer les nombres :
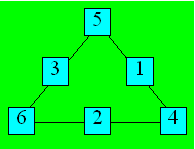
65. Étoile magique
Voici les quatre façons de distribuer les
nombres :
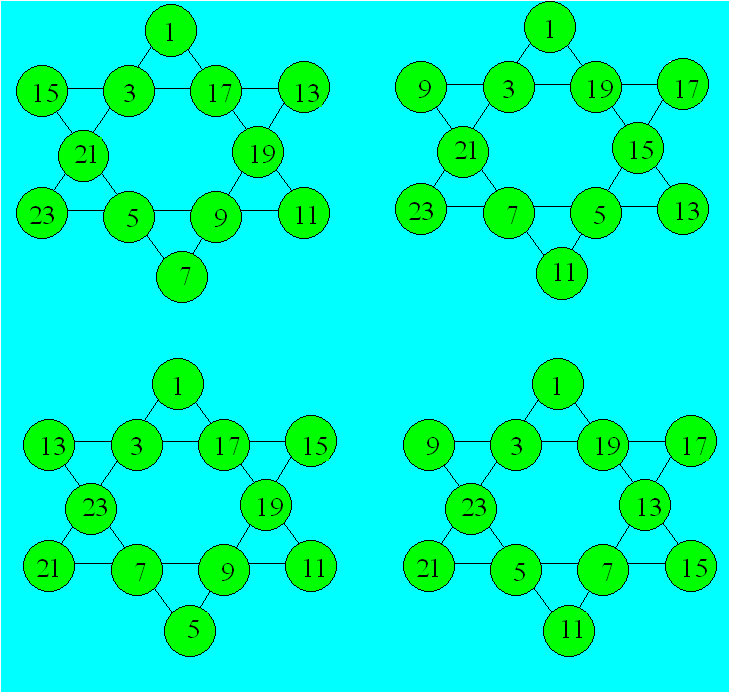
En considérant les figures obtenues par
rotation ou par réflexion et sans appliquer la contrainte des positions du 1 et
du 3, il existe 960 façons de placer les nombres impairs de 1 à 23.
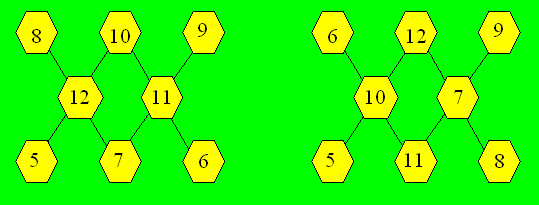
66. Un khi magique
Sans compter les configurations obtenues par
rotation ou par réflexion, on donne deux façons de distribuer les
nombres pour chaque somme :
a) La somme est 24.
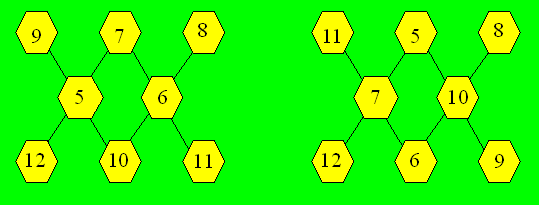
b) La somme est 27.
67. Un serpent
Il existe plus d'une façon de distribuer les
nombres. En voici une :
68. Cercles additifs
Voici une façon de distribuer les
nombres dans chaque cas :
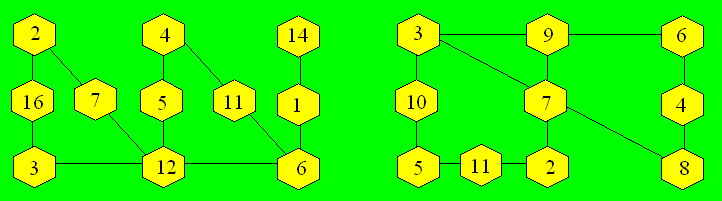
69. Addition magique
Voici une façon de distribuer les
nombres :
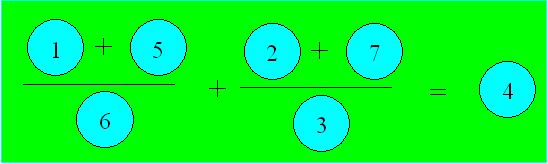
70. Un pavage magique
a) Voici une façon de distribuer les
nombres :

b) La somme des nombres consécutifs de
1 à 19 est 190. Chaque cellule est l'intersection de trois rangées. Cela
revient à écrire trois fois les nombres de 1 à 19 : ce qui donne 190 × 3 =
570. Comme on compte 15 rangées, on divise 570 par 15. Le résultat est bien
38. La somme sur chaque rangée est donc unique et égale à 38.
71. Sommes différentes
La configuration peut être trouvée à partir
de celle du problème précédent. Il s'agit de soustraire de 20 le nombre de
chaque cellule. La configuration est :

72. En amande
Il existe 32 façons de lire AMANDE.
73. Un tablier
On trouve 48 dispositions différentes.
74. Un carré latin partagé
Voici le carré complet :
|
1 |
9 |
8 |
2 |
|
8 |
2 |
1 |
9 |
|
2 |
8 |
9 |
1 |
|
9 |
1 |
2 |
8 |
75. En croix
Voici la grille
complétée :
|
1 |
4 |
5 |
6 |
2 |
3 |
|
3 |
2 |
6 |
5 |
4 |
1 |
|
4 |
5 |
3 |
1 |
6 |
2 |
|
6 |
3 |
2 |
4 |
1 |
5 |
|
2 |
6 |
1 |
3 |
5 |
4 |
|
5 |
1 |
4 |
2 |
3 |
6 |
76. Une grille croisée
Voici la grille
complétée :
|
6 |
3 |
5 |
7 |
2 |
4 |
1 |
|
1 |
5 |
7 |
2 |
4 |
6 |
3 |
|
2 |
6 |
1 |
3 |
5 |
7 |
4 |
|
3 |
7 |
2 |
4 |
6 |
1 |
5 |
|
4 |
1 |
3 |
5 |
7 |
2 |
6 |
|
5 |
2 |
4 |
6 |
1 |
3 |
7 |
|
7 |
4 |
6 |
1 |
3 |
5 |
2 |
77. Mathématique
Le mot MATHÉMATIQUE contient 12 lettres.
Si on divise 1000 par 12, on obtient 83 reste 4. Julie a donc écrit ce mot 83
fois. Elle est en train d'écrire la quatrième lettre du mot, soit H.
78. Tout pour 125
Voici une façon de remplir la grille :
|
1 |
2 |
5 |
1 |
|
2 |
1 |
1 |
2 |
|
5 |
1 |
2 |
5 |
|
1 |
2 |
5 |
5 |
79. Des chiffres à la suite
a) Le plus petit nombre de quatre chiffres est
1243.
b) Le plus grand nombre de quatre
chiffres est 9467.
|
|
|
Chapitre 3. Récréations
cryptarithmiques
80. Un cryptarithme
Pour résoudre un cryptarithme, on peut
utiliser deux stratégies : la déduction et un tableau du chiffre des unités.
En analysant la disposition des lettres, on peut déduire certaines valeurs. Par
la suite, on construit un tableau dans lequel on donne à une lettre choisie les
valeurs de 0 à 9. On place les lettres dont la valeur est connue. On trouve
ainsi la valeur de d'autres lettres. Il peut arriver qu'on ait besoin de faire
d'autres hypothèses sur une lettre choisie. Quand un chiffre est déjà
attribué à une lettre, on met ce chiffre entre parenthèses : ce qui signifie
que l'hypothèse de départ est rejetée.
Voici la démarche qu'on peut utiliser
pour résoudre le présent cryptarithme : Puisque (B + F) est égal à B, alors
F est égal à 0 et il n'y a pas de retenue. Puisque (H + H) est égal à H,
alors H est égal à 9 et D est égal à 1. On peut maintenant construire un
tableau en donnant à G les valeurs de 2 à 8. Le tiret indique qu'il ne peut
pas y avoir de solution dans cette colonne.
|
G |
(0) |
(1) |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
(9) |
|
B |
|
|
3 |
4 |
5 |
6 |
7 |
8 |
(9) |
|
|
C |
|
|
1 |
- |
2 |
- |
3 |
- |
|
|
|
A |
|
|
(9) |
|
8 |
|
(7) |
|
|
|
D’où, F = 0, D = 1, C = 2, G = 4, B =
5, A = 8 et H = 9.
81.
Quatre alphamétiques
Les égalités sont respectivement.
a)
9567 + 1085 = 10 652.
b)
407 + 700 + 9512 + 70 = 10 689
c)
73 544 + 73 544 + 73 544 + 494 046 = 714 678.
d)
7659 + 1089 + 1481 + 30 = 10 259.
82. Six un
UN est égal à 29. SIX vaut 174.
83. Paix ou guerre
TUE correspond à 285. ARMEE vaut 47 655.
84.
Rebondissements
Voici les deux égalités possibles :
a) 6352 + 8635 =
14 987. BONDS vaut 14 987.
b) 7354 + 8735
=16 089. BONDS vaut 16 089.
85. Quatre lettres
L’égalité est : 8910 + 891 = 9801. MARE
vaut 9801.
86. Tout en soleil
L’égalité est : 352 462 + 352 462 = 704
924. TREFLE vaut 704 924.
87. Chez Nitrou
L’égalité est : 96 233 + 62 513 = 158
746. La distance entre le logement et la discothèque est légèrement
inférieure à 1,6 kilomètre, plus exactement 1,58746 kilomètre.
88. Additions multiples
a) On trouve : 80 + 75 = 155, 19 + 64 = 83.
La somme est : 99 + 139 = 238.
b) On trouve : 83 + 38 = 121, 22 + 77 = 99. La
somme est : 105 + 115 = 220.
89. Produits croisés
La grille remplie est :
|
D4 |
U21 |
R18 |
|
O15 |
S19 |
A1 |
|
T20 |
E5 |
S19 |
90.
Le mot bionique
Les cinq meilleures
réponses dans l'ordre sont :
RACCROC
: 6 000 148
AVIATEUR
: 5 997 600
VOLATIL
: 6 005 760
CERCLE
: 5 976 432
QUARTES
ou TRAQUES : 6 032 880
91. Cercles chiffrés
Les chiffres correspondants à chaque lettre
sont :

92. Le mot codé
Les six lettres ayant le plus grand nombre de
points totalisent 87. Les lettres sont : B, O, P, R, S, T. Il existe une
quantité limitée de mots dont le code est supérieur à 80. En voici cinq :
APPORT, BOTTAS, PORTAS, PROPOS, RABOTS.
93.
Un nombre circulaire
On utilise : NOMBRE × E = SSSSSS.
À
cause de cette égalité où les chiffres des unités sont E × E = S, E ne peut
pas égaler 0, 1, 5 ou 6.
Si
E = 2, alors S = 4 : ce qui est impossible, car 444 444 ÷ 2 = 222 222.
Si
E = 3, alors S = 9 : ce qui est impossible, car 999 999 ÷ 3 = 333 333.
Si
E = 7, alors S = 9 et 999 999 ÷ 7 = 142 857.
Si
E = 8, alors S = 4 et 444 444 n'est pas divisible par 8.
Si
E = 9, alors S = 1 et 111 111 n'est pas divisible par 9.
Il y a une seule possibilité. NOMBRE
correspond à 142 857.
La réponse est : 341 162754 793 3579
841.
94. Grille symbolique
La grille remplie est :
|
8 |
8 |
8 |
24 |
|
8 |
8 |
8 |
24 |
|
8 |
8 |
8 |
24 |
|
24 |
24 |
24 |
72 |
95. Panneau de circulation
Le mot est BIENVENUE.
|
|
|
Chapitre 4. Récréations géométriques
96. Triangles et carrés
a) 24 triangles
b) 16 carrés
97.
Carrés de 36 cases
a) 25 carrés 2 ´
2
b)
16 carrés 3 ´ 3
c)
9 carrés 4 ´ 4
d)
4 carrés 5 ´ 5
e)
91 carrés de toute grandeur
98.
Carrés de 49 cases
a) 36 carrés 2 ´
2
b)
25 carrés 3 ´ 3
c)
16 carrés 4 ´ 4
d)
9 carrés 5 ´ 5
e)
4 carrés 6 ´ 6
f)
140 carrés de toute grandeur
99. Carrés de 64 cases
On compte 204 carrés de toute grandeur.
100. Quadrillage géant
De façon générale, le nombre de carrés de
toute grandeur est égal à (2n3 + 3n2
+ n)/6 où n est la mesure du côté du grand carré.
Si n est égal à 100, le nombre
de carrés est 338 350.
101. Allumettes
Voici une disposition des allumettes dans chaque
cas :
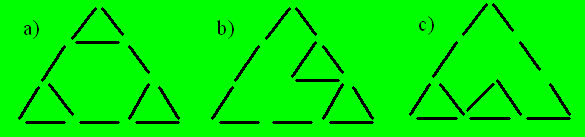
102. En lignes
Il existe plus d'une solution. En voici une :
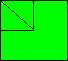
103. Dix droites
Voici une solution dans chaque cas en comptant
les petits et les grands carrés.
104. Des points
On trace d'abord un carré à partir d'un
coin. Puis, on complète chaque rangée horizontale en continuant sur la
rangée inférieure. On obtient ainsi 18 carrés qui sont numérotés.
|
1 |
2 |
|
3 |
|
|
|
4 |
5 |
6 |
7 |
|
8 |
9 |
10 |
11 |
|
|
|
12 |
13 |
14 |
15 |
|
16 |
|
17 |
|
18 |
Pourrait-on démontrer qu'il s'agit bien
du maximum ?
105.
Fantaisies chiffrées
7 segments : 16
8 segments : 17 - 1
9 segments : 42
10
segments : 4 × 4 11
segments : 15 + 1 12
segments : 17 - 1 × 1
13
segments : 14 + 2 14 segments : 112 ÷ 7 15 segments : 64 ÷ 4
106.
D'autres fantaisies chiffrées
a) 1 au lieu de 7
b) 12 au lieu de 38
c)
8 ÷ 8 au lieu de 4 ÷ 2
d) 9 au lieu de 5 ou vice versa
e)
= au lieu de - et vice versa
f) 8 au lieu de 6 et vice versa
107. Piste circulaire
Le diamètre de la piste est égal au côté du
terrain carré. D'où, l'aire est égale à 500 m × 500 m ou 250 000 m2.
108.
Un enclos
Il existe trois solutions. Les voici :
a)
15 et 25 mètres
b) 21 et 29 mètres
c) 48 et 52 mètres
109. Découpage
Voici une façon d’accoler les carrés :
110. Avec des diagonales
La croix oblique contient les cinq carrés. L’extérieur
de la croix est formé par 12 triangles.
111. Une planche de bois
André fait le trait de scie indiqué à gauche.
Par la suite, il place les deux morceaux comme il est montré à droite.
112. À trait continu
Voici une façon de partager le carré :

113. D'un à l'autre
Voici une façon de partager le carré :

114. Neuf droites
On dresse un tableau dans lequel le nombre de
parties est donné en fonction du nombre de segments.
|
Segments |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Parties |
2 |
3 |
5 |
8 |
12 |
17 |
23 |
On observe une régularité. Quand on ajoute un segment, le nombre de parties
augmente du nombre de parties du cas précédent. Le nombre de parties peut
s'écrire successivement : 2, 2 + 1, 2 + 1 + 2, 2 + 1 + 2 + 3, 2 + 1 + 2 + 3 +
4, 2 + 1 + 2 + 3 + 4 + 5, 2 + 1 + 2 + 3 + 4 + 5 + 6.
a)
Pour cinq segments, on a 12 parties.
b)
Pour six segments, on a 17 parties.
c)
Pour sept segments, on a 23 parties.
d)
Pour n segments, on devra avoir, selon cette régularité, 2 + 1 + 2 + 3
+ 4 + 5 +..... + (n - 1).
On
peut écrire : 2 + (n - 1)n/2 ou encore (n2
- n + 4)/2.
D'où, avec n droites, on peut
partager le cercle en un maximum de (n2 - n
+ 4)/2.
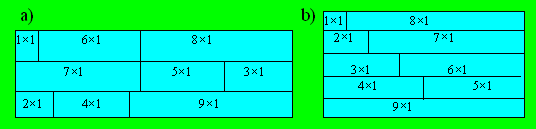
115. Champs rectangulaires
Voici un partage dans chaque cas :
116. Un potager
L'aire du terrain est de 6000 m2.
Si Armande en a 2x, alors Réjeanne en a 4x, Normand en a 6x
et Bertrand en a 3x : ce qui donne en tout 15x. D'où x est
égal à 400.
Armande a 800 m2,
Réjeanne 1600 m2, Normand 2400 m2
et Bertrand 1200 m2.

117. Terrain clôturé
Plus un terrain rectangulaire se rapproche d'un
carré, plus le périmètre est petit. Un terrain carré ayant une superficie de
896 mètres carrés aurait 29,93 mètres de côté. Le nombre entier le plus
près qui divise 896 est 28. D'où, le terrain mesure 28 mètres de largeur et
32 mètres de longueur.
118. À trait continu
Dans chacun des cas, les points de départ et
d'arrivée sont donnés.
119. Itinéraire
Il y a six chemins différents.
120. Un immeuble
Chaque pièce possède quatre portes sauf les
pièces D et I qui en contiennent trois. Si Renée part d'une pièce de quatre
portes, elle franchira d'abord une porte puis au retour deux autres : une pour
entrer et l'autre pour sortir. Il restera toujours une porte non franchie. D ou
I est une pièce de départ.
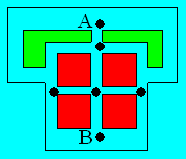
121. Des corridors
On compte le nombre d'issues à chaque point
carrefour. Les points A et B sont de degré impair. Il est possible de parcourir
le réseau en partant de A pour arriver à B ou de B à A.
122. En croisière
En ligne droite, le bateau parcourt une distance
égale au périmètre de l'île. Pour l'ensemble des quatre coins, il parcourt
une distance égale à la circonférence d'un cercle de 100 mètres de rayon.
Comme la circonférence est de 628
mètres, le périmètre de l'île est de 10 km - 628 m, soit approximativement
9,4 kilomètres.
123.
Arrêts temporaires
Il y a deux trajets possibles.
a)
AB, BD, DE, EB, BF
b)
AD, DE, EB, BC, CF
124. Silhouettes
Il existe quatre figures. Les voici :

125. En orbite
Le nombre qui reste est 3.
|
|
|
Chapitre 5.
Récréations logiques
126. Sous le signe des fleurs
Le tableau donne le
nom des fleurs et la saison préférée de chacun.
|
Noms |
André |
Daniel |
Michel |
|
Fleurs préférées |
lilas |
glaïeuls |
tulipes |
|
Signes du Zodiaque |
Taureau |
Lion |
Bélier |
|
Saisons préférées |
été |
printemps |
hiver |
Michel préfère les tulipes et l'hiver.
127. Riches et pauvres
Conrad est le plus pauvre.
128. Esprit de famille
Le tableau contient les coordonnées de chaque
garçon.
|
Nom des garçons |
Bernard |
David |
Fernand |
Louis |
Vincent |
|
Âge des garçons |
17 ans |
16 ans |
18 ans |
15 ans |
14 ans |
|
Nom des pères |
Robert |
Jean |
Stéphane |
Éric |
Laurent |
|
Nom des mères |
Anne |
Rose |
Berthe |
Martine |
Louise |
|
Numéro des rues |
12e rue |
8e rue |
3e rue |
10e rue |
7e rue |
Fernand, le fils de Stéphane, a 18 ans.
C'est Louis qui demeure sur la 10e rue.
129. Panier de boules
On pourrait utiliser une solution algébrique.
Toutefois, il s'avère intéressant d'appliquer les propriétés des nombres. La
masse de A ou de B ne peut pas être représentée par un nombre impair, car la
masse totale est paire. Il y a deux boules et une boule dans chaque proposition.
La masse est représentée par un multiple de 4, inférieure ou égale à 12,
car aucune ne peut être impaire. À cause de la première propriété, si A est
égal à 4 ou à 8, B est supérieur à 12. D'où, A est égal à 12 et B est
égal à 8.
La boule A a une masse de 12 kilogrammes
et la B a 8 kilogrammes.
130. Phrase codée
LES PARESSEUX ONT BEAUCOUP DE PROJETS MAIS PEU
DE RÉALISATIONS À LEUR CRÉDIT.
131. Phrase symbolique
UNE TEMPÊTE DE NEIGE EMPÊCHA TOUS LES ÉLÈVES
DE LA VILLE DE SE RENDRE EN CLASSE.
132. Triangle chiffré
Pour trouver une configuration, on peut
simplement écrire 1 au lieu de 0 et vice versa.
133. Jours de la semaine
a) VENDREDI : 5
b) SAMEDI : 4
c) JEUDI : 5
d) MERCREDI : 4
134. Le quatrième cercle
Le cercle complété est :
135. Le sixième dessin
Le sixième dessin est :

136. Les paradoxes
Ceci est un bel exemple de paradoxe. S'il dit
vrai, alors il est vrai que tout le monde est menteur. En conséquence, étant
menteur lui-même, il ne peut que mentir. S'il dit faux, alors personne n'est
menteur et comme il est citoyen de cette ville, il ne peut pas lui-même mentir
: ce qu'il vient de faire.
|
|
|
Chapitre 6.
Récréations et jeux
137. Seize cases
Voici une façon de
déplacer le cavalier dans chaque cas :
|
1 |
6 |
13 |
|
|
6 |
1 |
10 |
15 |
|
12 |
9 |
4 |
7 |
|
9 |
12 |
7 |
4 |
|
5 |
2 |
11 |
14 |
|
2 |
5 |
14 |
11 |
|
10 |
15 |
8 |
3 |
|
13 |
8 |
3 |
|
138. Vingt-cinq cases
Voici une façon de déplacer le cavalier dans
chaque cas :
|
1 |
24 |
13 |
18 |
7 |
|
14 |
1 |
18 |
7 |
|
|
14 |
19 |
8 |
23 |
12 |
|
19 |
8 |
15 |
12 |
17 |
|
9 |
2 |
25 |
6 |
17 |
|
2 |
13 |
4 |
21 |
6 |
|
20 |
15 |
4 |
11 |
22 |
|
9 |
20 |
23 |
16 |
11 |
|
3 |
10 |
21 |
16 |
5 |
|
24 |
3 |
10 |
5 |
22 |
139. Trente-six cases
On colorie les cases comme sur un échiquier.
À chaque mouvement, le cavalier passe
d'une case noire à une blanche, puis d'une blanche à une noire et ainsi de
suite. La case de départ, marquée 1, est noire ; celle marquée 2 sera blanche
; celle marquée 3 sera noire ; la 4 sera blanche, etc. Chaque case portant un
numéro impair est noire. Chaque case paire est blanche. Or, par rapport aux
données du problème, la case 36 est noire.
Il est donc impossible de trouver une
solution.
140. Quarante-neuf cases
Voici une façon de déplacer le cavalier :
|
3 |
40 |
25 |
48 |
23 |
38 |
21 |
|
26 |
49 |
4 |
39 |
20 |
47 |
36 |
|
5 |
2 |
41 |
24 |
37 |
22 |
19 |
|
42 |
27 |
6 |
1 |
18 |
35 |
46 |
|
7 |
10 |
29 |
12 |
33 |
14 |
17 |
|
28 |
43 |
8 |
31 |
16 |
45 |
34 |
|
9 |
30 |
11 |
44 |
13 |
32 |
15 |
141. Soixante-quatre cases
Voici une façon de déplacer le cavalier :
|
47 |
30 |
1 |
52 |
5 |
28 |
43 |
54 |
|
2 |
51 |
48 |
29 |
44 |
53 |
6 |
27 |
|
49 |
46 |
31 |
4 |
25 |
8 |
55 |
42 |
|
32 |
3 |
50 |
45 |
56 |
41 |
26 |
7 |
|
15 |
62 |
33 |
20 |
9 |
24 |
39 |
58 |
|
34 |
19 |
16 |
61 |
40 |
57 |
10 |
23 |
|
17 |
14 |
63 |
36 |
21 |
12 |
59 |
38 |
|
64 |
35 |
18 |
13 |
60 |
37 |
22 |
11 |
142. Le cavalier numérique
Voici une façon de déplacer le cavalier :
143. Le cavalier continu
Voici une façon de déplacer le cavalier :
144.
Erreurs de transcription
On fait :
17
au lieu de 20 18 au lieu de 21 19 au lieu de 22 20 au lieu de 23
21
au lieu de 24 22 au lieu de 25 23 au lieu de 26 24 au lieu de 27
25 au lieu de 28
La grille corrigée est :
|
1 |
26 |
9 |
32 |
7 |
24 |
|
10 |
31 |
18 |
25 |
16 |
33 |
|
19 |
2 |
27 |
8 |
23 |
6 |
|
28 |
11 |
30 |
17 |
34 |
15 |
|
3 |
20 |
13 |
36 |
5 |
22 |
|
12 |
29 |
4 |
21 |
14 |
35 |
148. Une somme chanceuse
Le tableau suivant indique les gains possibles
de chaque joueur. On voit que A a 5 chances de gagner, tandis que B en a 4. Le
jeu n'est donc pas équitable.
|
|
1 |
2 |
3 |
|
1 |
A |
B |
A |
|
2 |
B |
A |
B |
|
3 |
A |
B |
A |
151.
Master Mind
On suppose que le code est A, B, C , D dans l’ordre.
A
ne peut pas être bleu à cause des indices des rangées 2 et 3.
D
ne peut pas être vert à cause des mêmes indices.
B
est bleu et C est vert par déduction et à cause des indices de la rangée 2.
Il
n'y a pas de rouge et de noir à cause de la rangée 3.
Les
deux couleurs manquantes sont jaune et blanc, à cause de la rangée 1.
D'où,
D est jaune et A est blanc.
Le code est : blanc, bleu, vert, jaune.
|
|
|
Chapitre 7.
Récréations électroniques
152. Un cours
Le nom du cours est BIOLOGIE. Après avoir fait
les calculs, on fait faire une rotation de 180 degrés à la calculatrice.
153. Une somme
Voici une démarche possible : on suppose que la
somme pourrait être 10 000. Alors, on inscrit 10 000 et on soustrait chacun des
nombres de la grille.
10 000 - 564 - 939 - 888 - 465 - 993 -
777 - 456 - 399 - 666 = 3853.
On soustrait de 10 000 le résultat
obtenu : 10 000 - 3853 = 6147. La somme est 6147.
154. Quatre opérations
On fait successivement ces opérations :
1994 - 24 = 1970, 1970 × 24 = 47 280, 47 280 + 24 = 47 304, 47 304 ÷ 24 =
1971.
158. Le cent de Lucas
Voici les quatre expressions dans chaque
cas :
a) 94 1578/263, 96 2148/537, 96 1752/438
et 96 1428/357.
b) 3 69258/714, 81 7524/396, 81 5643/297
et 82 3546/197.
159. Un organigramme
Soit x le nombre choisi. Si (2x -
10) est plus petit que 19, alors x est plus petit que 14,5 et le
résultat final est 0. Si (2x - 10) est plus grand que 19, alors x
est plus grand que 14,5. Dans ce cas, x doit être plus petit que 19,5.
Les nombres de départ sont : 15, 16,
17, 18 et 19.
160. Un autre organigramme
Soit x le nombre choisi. Si 2x est
plus petit que 25, alors x est plus petit que 12,5. Dans ce cas, (2x
+ 12 - x) ou (x + 12) est supérieur à 10 et le résultat final
est 9. D'où, x doit être plus grand que 12,5. Si x est plus
grand que 12,5, on a : (2x - 6)3/6 ou (x - 3).
Si (x - 3) est plus petit ou
égal à 25, alors x est plus petit ou égal à 28. Dans ce cas, on a : (x
- 3 + 12 - x) ou 9. Il faut que x soit plus grand que 28.
Le plus petit nombre est 29.
|
|
|
Chapitre 8.
Recherches récréatives
161.
Le calendrier
a) Le 31 janvier 1933 : mardi
b)
Le 2 juin 1945 : samedi
c)
Le 19 octobre 1958 : dimanche
d)
Le 24 novembre 1978 : vendredi
e)
Le 3 mai 1988 : mardi
f)
Le 1 janvier 2000 : samedi
162. La famille des nombres
Les trois nombres sont:
33 + 73 + 03
= 370
33 + 73 + 13
= 371
43 + 03 + 73
= 407
163.
Des nombres narcissiques
Les nombres peuvent être représentés
ainsi :
122 + 332 =
1233,
14 + 64 + 34
+ 44 = 1634,
882 + 332 =
8833.
164.
Des chaînes
Voici deux chaînes :
55
: 53 + 53 =
250, 250 : 23 + 53
+ 03 = 133, 133 : 13
+ 33 + 33 = 55
136 : 13
+ 33 + 63
= 244, 244 : 23 + 43
+ 43 = 136
165.
Puissances en ordre
Voici trois nombres :
135
= 11 + 32 + 53
175 = 11 + 72
+ 53
518 = 51 + 12
+ 83
166.
Variations sur 1987
Dans chacun des cas, il existe d'autres façons
de distribuer les chiffres :
a)
3 = 1 + (9 + 7) ÷ 8
4 = 91 - 87
5 = 7 - 18 ÷ 9
6
= 7 + 8 - 9 × 1
7 = 1 + 7 + 8 - 9
8 = 7 + (1 + 8) ÷ 9
9
= 7 + 18 ÷ 9
10 = (1 + 9) ÷ (8 - 7)
b)
3 = 1 + Ö9 - 8 + 7
4 = 19 - 8 - 7
5 = Ö1+9+8+7
6
= -1 × 9 + 8 + 7
7 = 1 - 9 + 8 + 7
8 = 198 + 7
9
= (1 × 9)(8 - 7)
10 = 1(9 + 8 - 7)
c)
(333 × 3!) - 33/3
44Ö4
+ 44 + 4 + 4 - 4/4
5!
× (5 + 55/5) + 55 + 5! ÷ (5 + 5)
666
× (6 + 6 + 6)/6 - (6 + 6 - 6/6)
d) 19(99 + 999/999) + 88 - 8 + (8 + 8 + 8 + 8)/8 + (7 + 7 +
7 + 7)/7 - 7/7
e) 9 + 8 + 7 + (654 × 3) + 2 - 1
167.
Un problème de divisibilité
L'expression n'est pas divisible par 2,
car 2100 est un nombre pair et 3100
est un impair.
L'expression
n'est pas divisible par 3, car 3100 est
divisible par 3 et 2100 ne l'est pas.
L'expression
n'est pas divisible par 4, car elle n'est pas divisible par 2.
L'expression
n'est pas divisible par 5 car, d'après la colonne 3 du tableau, seuls les
nombres de puissance impaire sont divisibles par 5.
L'expression
n'est pas divisible par 6, car elle n'est pas divisible par 2 et par 3.
L'expression
n'est pas divisible par 7. Lorsque n = 3 ou 9, la somme est divisible par
7. Il en est de même pour les nombres de la suite 3, 9, 15, 21, etc. Lorsque n
est pair, le résultat ne peut pas être divisible par 7.
L'expression
n'est pas divisible par 8, car elle n'est pas divisible par 2.
L'expression
n'est pas divisible par 9, car elle n'est pas divisible par 3.
L'expression
n'est pas divisible par 10, car elle n'est pas divisible par 2 et par 5.
168. Nouvelle approche de la parité
a) Tout nombre pair de la classification
traditionnelle est également pair. De même, tout nombre impair est également
impair. La règle de classification consiste à considérer pairement égal à (´
2) et impairement égal à (´
2 + 1) ; puis, à effectuer des multiplications à partir du dernier résultat .
Dans le cas présent, on procède ainsi :
impairement
: 2 + 1 = 3
impairement
: 3 × 2 + 1 = 7
impairement
: 7 × 2 + 1 = 15
impairement
: 15 × 2 + 1 = 31
pairement
: 31 × 2 = 62
pairement
: 62 × 2 = 124
impair
: 124 × 2 + 1 = 249
Le nombre cherché est 249.
b) 41, 101, 694, 1400
c) 12 : I P P
19 : P P I I
48 : I P P P P
145
: P P I P P P I
167 : P I P P I I I
501 : I I I I P I P I
169.
Les nombres décubés
a) 49
b) 262 080
c) 999 900
d) 6 nombres décubés
e)
704 880 f) non
g) 79 464
h) 6
i)
Voici quatre propriétés :
1.
Les nombres décubés sont toujours formés par le produit de trois entiers
consécutifs.
2.
Les nombres décubés se terminent par 0, 4 ou 6.
3.
La somme réduite des nombres décubés est toujours 3, 6 ou 9. Exemple. La
somme réduite de 12 144 est 3 car 1 + 2 + 1 + 4 + 4 = 12 et 1 + 2 = 3.
4.
À toute racine de même unité correspond un ensemble de nombres décubés de
même unité. Exemple. Lorsque la racine se termine par 7, le nombre décubé
se termine par 6.
|
|
FIN
|
![]()
![]()