|
| |
|

|
Publications |
|
Ceci est le septième livre édité par Récréomath.
Au jeu
Par Charles-É. Jean
|
* * *
* * * * * * *
Avant-propos
| Les
programmes de mathématiques au secondaire, comme d'ailleurs au
primaire, s'orientent vers la résolution de problèmes. L'élève est
amené à appliquer ses connaissances en mathématisant des situations.
Après avoir transformé les données par des opérations appropriées,
il doit vérifier et interpréter les résultats obtenus.
Les problèmes et les textes de ce recueil ont été
conçus et présentés dans cette optique. Les mathématiques
récréatives puisent des faits et des événements dans la vie
quotidienne. Le support mathématique permet des transformations et des
opérations qui se situent dans un contexte global de résolution de
problèmes. Le tout est vu sous un aspect divertissant et récréatif.
Une récréation mathématique se présente
généralement sous forme d'un texte qui décrit une situation et pose
une interrogation en regard des conditions. Parfois, du matériel de
manipulation peut être fabriqué en relation avec les données. Le
temps pour arriver à la réponse n'est pas déterminé et il n'y a pas
de compétition. La démarche de résolution doit être la plus
raffinée possible. Les exigences mathématiques sont très variables.
En tout temps, la réflexion, la perspicacité et la logique doivent
intervenir.
Les récréations et textes de ce recueil ont d'abord
été publiés dans la revue Envol du GRMS de mars 1978 à juin
1988. Ils ont été regroupés en différents chapitres selon leur
contenu mathématique. Les récréations et solutions ont été revues
et améliorées en adaptant davantage la formulation en rapport avec le
processus de résolution de problèmes. Cette nouvelle présentation
permet davantage à l'élève de réaliser une démarche autonome. De
plus, les enseignantes ou enseignants pourront utiliser ce matériel
dans leur enseignement ou pour des activités complémentaires.
À un moment ou l'autre, l'élève a besoin de doses
d'imaginaire, de réel et de rationnel. Une exploitation des
récréations et de la recherche permet de développer des habiletés
qui vont motiver l'élève à comprendre, à communiquer, à résoudre
et à produire des problèmes. Dans ce cadre, le matériel a une portée
plus organique et il favorise la réceptivité qui peut naître de la
fascination.
Nous souhaitons aux utilisatrices et utilisateurs des
récréations et des textes de ce recueil qu'ils puissent voir la
richesse des mathématiques dans un contexte récréatif et qu'ils
puissent vivre des moments de délectation, de curiosité et de
triomphe.
Charles-É. Jean |
* * * * * * *
Chapitre 1
Récréations numériques
|
Partie A.
Addition et soustraction
1. Plus ou moins
En intercalant les signes + ou - entre les
chiffres 1, 2, 3, 4, 5, 6 et 7 sans changer leur ordre et en les accolant s'il y
a lieu, on peut obtenir, par exemple, 31 comme résultat.
12 - 3 - 45 + 67 = 31
Trouvez 23 comme résultat en suivant
les mêmes règles et en utilisant deux nombres de deux chiffres et trois
nombres d'un seul chiffre.
2. Quatre groupes
Partagez les nombres de cette grille en quatre
groupes de sorte que la somme des quatre nombres de chaque groupe soit
identique.
|
1 |
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
|
9 |
10 |
11 |
12 |
|
13 |
14 |
15 |
16 |
3. Chiffres uniques
L'égalité suivante utilise les chiffres de 1
à 9 pris chacun une seule fois.
39 + 45 + 78 = 162
Trouvez une autre façon de répartir
ces chiffres de telle manière que la somme de trois nombres de deux chiffres
est égale à un nombre de trois chiffres.
4.
Nombres de trois chiffres
Trouvez trois nombres entre 100 et 1000 qui ont
les propriétés suivantes.
·
Ils sont formés par les chiffres de 1 à 9
pris chacun une seule fois.
·
Leur somme est 1665.
·
La différence des deux plus grands est
324.
·
La somme des chiffres de chaque nombre est
15.
5. Des timbres cachés
Étienne a disposé 10 cases comme ci-après
pour placer ses 1136 timbres. Le nombre de timbres de chaque case des trois
rangées supérieures est égal au total des timbres qui se trouvent dans les
deux cases inférieures adjacentes. Étienne connaît le nombre de timbres de
trois cases : 45, 43 et 347. Par exemple, si Étienne plaçait 12 timbres dans
la deuxième case de la rangée inférieure, il devrait y en avoir 57 dans la
première case de la deuxième rangée.

Trouvez le nombre de timbres dans
chacune des cases vides.
6. Une somme
Avec chacun des chiffres 1, 2, 3 et 4, on peut
écrire 3214, 4312, 1324, etc.
Déterminez la somme de tous les nombres
formés de ces quatre chiffres.
7. En progression
Quatre nombres sont placés dans chacune des
deux grilles ci-après.
Complétez chacune des grilles. Dans
chaque ligne et dans chaque colonne, les nombres doivent être en progression
arithmétique, c'est-à-dire que la différence entre deux termes voisins doit
être la même dans chaque rangée. Par exemple, 4, 10, 16, 22 forment une
progression arithmétique. La différence entre chaque terme est 6.
8. Un cycle
Quatre nombres sont placés dans le premier
diagramme. En additionnant trois par trois les nombres qui se suivent à partir
de chacun des cercles, on obtient successivement 9, 12, 10 et 8.
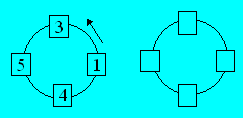
Dans le second diagramme, inscrivez
quatre nombres dont les sommes par groupe de trois sont successivement 10, 11, 6
et 12.
9. Pyramides de nombres
Dans la pyramide de base 4 ci-dessous, des
nombres sont inscrits selon la règle suivante. Chaque nombre des rangées
supérieures est la somme des deux nombres inférieurs adjacents. Ainsi, 24
placé dans la première case de la troisième rangée est la somme de 13 et de
11, deux nombres qui lui sont adjacents. La case supérieure est appelée sommet
et les quatre cases inférieures forment la base.
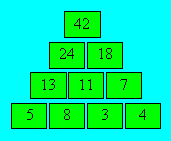
a) Construisez cinq pyramides dont les
sommets sont successivement 34, 36, 38, 44, 46 et dont la base contient 3, 4, 5
et 8.
b) Identifiez le plus petit sommet et le
plus grand sommet d'une pyramide dont la base contient 6, 7, 8 et 9.
c) Si on considère qu'une pyramide est
différente d'une autre dès qu'au moins un nombre de chacune des quatre
rangées est différent, trouvez le nombre de pyramides qui peuvent être
construites si la base est formée de 5, 8, 11 et 13.
d) Construisez une pyramide de base 3
dont la somme des éléments de la base est 48 et dont le sommet est 63.
e) Construisez une pyramide de base 4
dont la somme des éléments de la base est 120 et dont le sommet est 136.
f) Complétez la pyramide suivante :
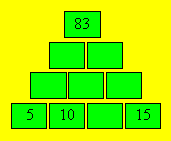
|
|
|
Partie B. Multiplication et
division
10. L'intersection
Dans les cases, placez les nombres 7, 10, 12,
15, 16, 19, 21, 22 et 40 selon les indications données à gauche et en haut de
la grille.
|
|
Nombre divisible
par 5 |
Nombre plus
grand que 18 |
Nombre plus
petit que 18 |
|
Nombre divisible
par 3 |
|
|
|
|
Nombre entre
5 et 20 |
|
|
|
|
Nombre pair |
|
|
|
11. Numéros de rues
Deux amis demeurent à 12 rues d'intervalle dans
une ville où les rues portent un numéro dans l'ordre. Si on multiplie les deux
numéros de rue l'un par l'autre, on obtient 589.
Sur quelles rues demeurent les deux amis
?
12.
Divisibilité par 7
Trouvez un nombre de neuf chiffres
·
qui est divisible par 7.
·
dont les cinq premiers chiffres sont 1, 2,
3, 4 et 5 dans cet ordre.
·
qui est composé des chiffres 1 à 9 pris
chacun une seule fois.
13. Vers le million
Quel est le plus grand nombre inférieur à 1
000 000 qui est divisible par les nombres successifs de 2 à 19 ?
|
2 |
|
11 |
|
|
3 |
|
12 |
|
|
4 |
|
13 |
|
|
5 |
|
14 |
|
|
6 |
|
15 |
|
|
7 |
|
16 |
|
|
8 |
|
17 |
|
|
9 |
|
18 |
|
|
10 |
|
19 |
|
14. En cercles
Placez quatre nombres
dans le diagramme. Les produits par groupe de trois nombres voisins doivent
être successivement 60, 70, 84 et 210.
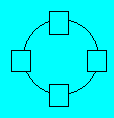
15. L'avoir de Nathalie
Nathalie possède un montant inférieur à 59 $.
Si elle veut partager également cette somme entre ses six amies, il lui reste 5
$. Si elle veut faire le partage entre cinq amies, il lui reste 4 $.
Quel est l'avoir de Nathalie en dollars
entiers ?
16.
Montants doubles
Jules et Judith possèdent chacun un montant
entre 100 $ et 600 $. Judith a le double de Jules. Dans l'écriture des deux
montants, on retrouve les chiffres de 0 à 5 pris chacun une seule fois.
-
Eurêka, s'écrit Éric, Jules a 152 $ et Judith a 304 $.
Cette réponse est bonne ; mais ce ne
sont pas les avoirs de Jules et de Judith.
Quels sont ces avoirs ?
17. Une table de multiplication
En voyant la table de multiplication des nombres
de 1 à 12, Noël s'est demandé combien il y manquait de nombres entre 0 et
144. Aidez-le à résoudre ce problème.
|
× |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Partie C. Quatre
opérations
18. Itinéraire
À partir de A qui est
égal à 12, il s'agit de se rendre jusqu'à B en passant par tous les nombres
et en faisant une addition ou une soustraction. Quand on atteint le symbole J,
on fait une multiplication ou une division avec le nombre suivant.
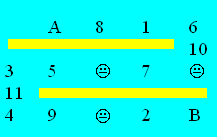
Trouvez une chaîne d'opérations qui
donne 16 comme résultat final.
19. Les jeans d'Éric
Dans sa boutique, Éric vend quatre marques de
jeans : les Axès, les Bexès, les Cexès et les Dexès.
Le coût de chaque jeans a été fixé
pour correspondre au nombre de paires en inventaire au début du solde. Ce coût
varie entre 23 et 42 euros. Ainsi, s'il y avait 26 paires de jeans en
inventaire, le prix est de 26 euros. Les jeans Dexès coûtent plus chers que
les Axès et moins chers que les Cexès. De plus, chaque marque a un prix
différent.
Quand tous les jeans ont été vendus,
Éric a remarqué que le résultat de la vente des jeans Axès et Bexès
ensemble a été le même que celui des jeans Cexès et Dexès ensemble.
Combien y avait-il de jeans de chaque
marque en inventaire au début du solde ?
20. Un mois de novembre
C'est le vendredi 20 juin 2014. En se promenant
sur la grève, Jasmine trouve dans un étui fabriqué en 2006 une feuille de
calendrier correspondant au mois de novembre.
|
D |
L |
M |
M |
J |
V |
S |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
29 |
30 |
|
|
|
|
|
De quelle année s'agit-il ?
21. Avec 1982
Les chiffres de 1982 sont déjà placés dans
les cases.
|
1 |
|
9 |
|
8 |
|
2 |
= |
1 |
|
1 |
|
9 |
|
8 |
|
2 |
= |
9 |
|
1 |
|
9 |
|
8 |
|
2 |
= |
8 |
|
1 |
|
9 |
|
8 |
|
2 |
= |
2 |
Intercalez entre chaque case un des
signes des quatre opérations de façon à obtenir le résultat indiqué à
droite.
22.
Beaucoup de 7
Des nombres possèdent les propriétés
suivantes.
·
Ils sont divisibles par 7.
·
Leur dernier chiffre est 7.
·
La somme réduite de leur chiffre est 7.
Par exemple, la somme réduite de 358 est 7, car 3 + 5 + 8 = 16 et 1 + 6 = 7.
Combien y a-t-il de nombres entiers
supérieurs à 7 et inférieurs à 7777 qui possèdent les propriétés données
?
23. Une astuce de calcul
Jocelyne fait les achats suivants : un couteau
tout usage à 6,39 $ ; deux poêles à 12,99 $ chacune ; six bols à mélanger
à 2,98 $ chacun ; trois moules à gâteau dont elle ignore le prix
unitaire.
La caissière enregistre les achats et
annonce à Jocelyne que le montant total, avant la taxe de vente, est de 56,90
$. Immédiatement, Jocelyne proteste et dit à la caissière qu'elle s'est
trompée. La caissière vérifie. Jocelyne a raison.
Comment Jocelyne a-t-elle pu déceler
une erreur sans faire l'addition ?
24. Des cases vides
En utilisant les nombres 6, 10, 12, 15, 16, 18,
20, 21, 25, 35, 36, 54 et 75, remplissez les cases vides de telle manière qu'il
y a un nombre dans chaque case.
|
|
est le carré de |
|
|
|
est le nombre qui suit |
|
|
|
est le double de |
|
|
|
est inférieur de 10 à |
|
|
|
est le renversé de |
|
|
|
est le triple de |
|
À la fin, il restera un nombre. Quel
est ce nombre ?
25. Chemin d'opérations
En passant par certaines cases non grisées une
seule fois et en faisant les opérations indiquées, trouvez un chemin qui donne
20 comme résultat. Vous devez partir de 7 et vous déplacer toujours vers une
case adjacente.
|
7 |
- |
8 |
|
5 |
|
+ |
|
× |
9 |
× |
|
5 |
÷ |
3 |
+ |
7 |
|
|
2 |
+ |
4 |
|
26. L'âge de Sextus
Sextus est un humanoïde qui vit dans une
contrée retirée appelée Tryptus. Pour ses menus travaux, Sextus possède
trois bras ayant chacun deux doigts. Ayant appris l'arithmétique sur ses
doigts, Sextus compte ainsi :
|
1,
2, 3, 4, 5,
10,
11, 12, 13, 14, 15,
20,
21, 22, 23, 24, 25,
30,
31, 32, 33, 34, 35,
40,
41, 42, 43, 44, 45,
50,
51, 52, 53, 54, 55,
100,
101, 102, 103, 104, 105,
110,
111, etc. |
Sextus a inscrit son âge sur une
tablette près de son habitation. On y lit 12 243 ans.
Quel est l'âge de Sextus dans notre
numération ?
27. Pair et impair
Je suis un nombre pair situé entre 50 et 90. Si
on m'ajoute mon nombre renversé (exemple : 26 et 62), on obtiendra comme
résultat un nombre impair divisible par 5.
Qui suis-je ?
28. Mur de briques
Sur le mur de briques de gauche, on peut lire de
haut en bas huit nombres de quatre chiffres adjacents : 1247, 1248, 1258, 1259,
1358, 1359, 1369, 1360.
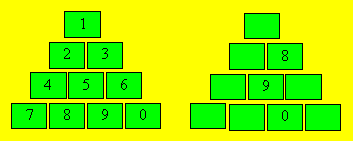
Complétez le mur de droite de telle
manière que chaque nombre lu est divisible par 7 et que la somme des huit
nombres soit 12 068.
29. Commerce de légumes
Romain décide d'investir tout son avoir dans un
commerce de légumes. La première année, il réalise un profit de 1500 $. La
seconde année, il a une perte de 300 $ et la troisième, une perte de 200
$.
Pendant les années suivantes, ses
profits et ses pertes se succèdent dans le même ordre et avec les mêmes
montants. Quand il prend sa retraite à la fin de sa 35e année, son avoir est
de 20 000 $.
Quel était l'avoir de Romain lorsqu'il
décida d'investir ?
30. À la renverse
La somme de deux nombres est composée de deux
chiffres identiques. L'un des nombres est le renversé de l'autre (exemple : 27
et 72). Le chiffre des centaines du produit des deux nombres est 4 et l'unité
est 2.
Quels sont ces deux nombres ?
31. Vers 25
En utilisant les opérations nécessaires,
représentez 25 au moyen du nombre des chiffres de la première colonne.
|
cinq 2 |
|
|
cinq 3 |
|
|
six 4 |
|
|
quatre 5 |
|
32. Tiers et quarts
Quel est le nombre dont les deux tiers
augmentés de 12 égalent les trois quarts diminués de 10 ?
33. Anniversaires
Émilie est née le 29 février 1880 et est
décédée le 5 novembre 1955.
Combien a-t-elle fêté d'anniversaires
de naissance le 29 février ?
34.
Faites votre choix
Vrai ou faux ?
a)
La somme de 19 nombres consécutifs est toujours divisible par 19.
b)
Le dernier chiffre du nombre correspondant à 444 est 4.
c)
Le nombre 1001 est divisible par trois nombres premiers consécutifs.
35. D'un à l'autre
|
+ 4 |
- 5 |
× 2 |
× 3 |
+ 6 |
- 3 |
¸ 2 |
a) Vous prenez le nombre 25. Vous
utilisez quatre opérateurs parmi les sept donnés pour obtenir 31. Quels sont
ces opérateurs ?
b) Le nombre de départ et le nombre
d'arrivée doivent être 29. Déterminez les quatre opérateurs utilisés.
c) Trouvez le plus grand résultat en
utilisant les sept opérateurs si le nombre de départ est 10.
36. Des oeufs
a) Une demi-douzaine de douzaines d'oeufs de
classe A coûte 5,68 $ et un oeuf.
Combien coûte une douzaine d'oeufs de
classe A ?
b) Douze douzaines d'oeufs de classe B
coûtent 10,35 $ et une demi-douzaine d'oeufs.
Combien coûte une douzaine d'oeufs de
classe B ?
37.
Dissections
Trouvez le nombre qui est le produit des trois
résultats suivants.
·
Je prends un septième de ce même nombre,
auquel je soustrais 63.
·
Je prends un quatorzième de ce même
nombre, auquel je soustrais 35.
·
Je prends un vingt-et-unième de ce même
nombre, auquel je soustrais 24.
38.
Avec 1985
En utilisant les opérations requises et les
quatre chiffres de 1985, chacun une seule fois, trouvez successivement les
résultats donnés.
·
3
·
6
·
12
·
18
39. En paires
En utilisant les nombres donnés dans le
tableau, remplissez les cases vides de telle sorte qu'il y ait un nombre dans
chaque case.
Deux nombres dont la somme est 44 et
dont la différence est 8.
Deux nombres dont la somme est 27 et
dont le produit est 176
Deux nombres dont la différence est 21
et dont le produit est 196.
À la fin, il restera un nombre. Quel
est ce nombre ?
|
|
|
Partie D.
Racines et puissances
40. Avec 1978
Utilisez les chiffres 1, 9, 7 et 8 chacun une
seule fois. Vous choisissez parmi les opérations d'addition, de soustraction,
de multiplication, de division, d'extraction de la racine carrée et
d'élévation à une puissance.
Vous devez obtenir les résultats de 40
à 49.
Exemple : (19 - 8) × 7 = 77
41. Avec 1986
Utilisez les chiffres 1, 9, 8 et 6 chacun une
seule fois. Vous choisissez parmi les opérations d'addition, de soustraction,
de multiplication, de division et d'extraction de la racine carrée.
Vous devez obtenir les résultats de 1
à 10.
Exemple : 6(8 + 1) ÷ Ö9
= 18
42. Divisibilité par 5
Parmi les expressions suivantes,
laquelle ou lesquelles sont divisibles par 5 ?
a) 4320
+ 4220
b) 4320 × 4220
c) 4320
- 4220
d) 4320 ÷ 4220
43. Extractions
Trouvez un nombre entier entre 1000 et 10 000
dont on peut extraire la racine carrée, la racine cubique et la racine
quatrième.
44.
Dernier chiffre
Quel est le dernier chiffre du nombre
correspondant à
a)
257
b)
4150
c)
7200
45. Nombres croisés
Dans la grille ci-après, il faut lire huit
nombres de quatre chiffres dont quatre nombres horizontalement et quatre
verticalement. On trouve, entre autres, dans la grille un seul 0, un seul 1, un
seul 6 et pas de 5.
En utilisant les définitions données
pour chaque ligne et chaque colonne, remplissez la grille.
A : a2
B : ab
C : a2 + 11a
D : 49a + 65
E : a2 - 5a
F : (a + 8)2
G : 100a + 3
H : 182b + 40
46. Tout en carré
Voici une égalité curieuse :
552 +
562 + 572 +
582 + 592 +
602 = 612 +
622 + 632 +
642 + 652
Existe-t-il d'autres cas où la
somme des carrés de n nombres consécutifs est égale à la somme des
carrés de (n - 1) nombres consécutifs ?
On assume que le premier nombre du
deuxième membre de l'égalité est également consécutif au dernier nombre
du premier membre.
47. Au hasard
Ce jeu peut devenir passionnant si on parvient
à déjouer le hasard. Il s'agit de choisir six nombres au hasard entre 0 et
30. On utilise les cinq premiers nombres et les opérations nécessaires de
façon à trouver le sixième nombre.
Les opérations peuvent être :
l'addition, la soustraction, la multiplication, la division et l'extraction de
la racine carrée.
Exemple : Avec les nombres 4, 7, 12,
13, 19 et avec 26 comme résultat, on peut écrire : (12 × 7 ÷ 4 - 19)13 =
26.
a) Utilisez les nombres 4, 5, 17, 21,
22. Le résultat 15.
b) Utilisez les nombres 2, 4, 7, 8,
22. Le résultat 3.
c) Utilisez les nombres 3, 8, 12, 16,
27. Le résultat 15.
d) Utilisez les nombres 3, 6, 7, 10,
12. Le résultat 1.
48.
Une charade
Mon premier est un carré parfait de deux
chiffres.
Mon
second est un carré parfait d'un seul chiffre.
Mon
tout est un carré parfait de trois chiffres.
Quel
est mon tout ?
|
|
Voir Chapitre 2.
Récréations combinatoires
|
![]()
![]()