En choisissant dans l'ordre 2, 5, 4, 1
et 5, la phrase serait : Mon frère détruit la
sculpture.
Le texte suivant a été composé par
ordinateur à partir de d’autres structures de phrases :
Le
bocage mélancolique
aime
cette pluie.
Avec
le nuage,
la
rivière tranquille
secoue
la lune.
Ma
mer spasmodique
gaspille
cette rivière
sous
le pêcheur.
Parce
que la fumée
noie
son coeur splendide,
la
nuit fragile
guide
son sommeil.
Analysez les différentes structures de
phrases. En vous inspirant de celles-ci ou encore en en ajoutant d'autres,
amusez-vous à composer des poèmes.
Vous pouvez faire le même travail sans
ordinateur. Il s'agit à ce moment d'utiliser des dés ou des jetons numérotés
pour faire au hasard le choix des mots de la banque que vous avez montée.
156. Projets avec l'ordinateur
Voici quelques idées de projets que vous pouvez
réaliser avec une connaissance minime d'un langage de programmation :
a)
Dessins et impressions
Construire
des figures géométriques.
Construire
des dallages ou mosaïques.
Représenter
un véhicule qui circule à une vitesse donnée.
b)
Apprentissages
Distinguer
les sortes de triangles.
Présenter
des exercices sur les quatre opérations.
Distinguer
des ensembles de nombres.
c)
Arithmétique
Additionner
un intervalle de nombres naturels.
Identifier
le plus grand nombre dans un tableau.
Convertir
les nombres en chiffres romains.
d)
Problèmes récréatifs
Construire
un biorythme.
Composer
des carrés magiques ou différentes figures magiques.
Construire
des labyrinthes.
e)
Jeux de société
Imaginer
un jeu de dés.
Composer
un jeu du pendu.
Composer
des jeux de nombres ou de mots.
157. Micro-problèmes
Voici quelques problèmes qui peuvent être
résolus par ordinateur :
a) Composez un programme le plus court
possible qui génère cinq nombres naturels de 100 à 1000 sans utiliser la
fonction hasard.
b) Composez un programme qui choisit des
nombres naturels au hasard, par exemple, entre 0 et 400. L'exécution s'arrête
quand le nombre que vous avez identifié a été atteint par l'ordinateur. Le
programme devra indiquer le rang où apparaît ce nombre.
c) Composez un programme qui permet de
faire la somme des nombres pairs entre 1 et 200, sans utiliser la touche + dans
le programme.
d) Composez un programme qui permet de
savoir s'il existe, entre 100 000 et 1 000 000, des nombres de la forme ABC ABC
(deux tranches identiques de trois chiffres) qui ne sont pas divisibles par 7.
e)
Composez un programme qui permet de trouver et d'imprimer les 1000 premiers
nombres naturels qui ont les propriétés suivantes :
·
ils sont divisibles par 7 et par 11.
·
ils ne sont pas divisibles par 3 et par 5.
f) Composez un programme qui permet de
trouver et d'imprimer tous les nombres palindromes compris entre 100 et 1 000
000. À titre d'exemples, 111, 535, 4664, 82 328, 743 347 sont des nombres
palindromes, car ils ont la même valeur si on les lit dans un sens ou dans
l'autre.
g) Composez un programme qui permet de
trouver et d'imprimer les 1000 premiers nombres premiers. (Idée de Jean-Guy
Sanche)
Aucune solution n’est donnée.
158. Le cent de Lucas
Dans son Arithmétique amusante écrite
en 1888, Édouard Lucas mentionne que le nombre 100 peut s'écrire sous forme
d'un entier et d'une fraction ordinaire de sept façons différentes en
utilisant chacun des chiffres de 1 à 9.
Voici trois de ses expressions :
91 5742/638
91 7524/836 91 5823/647
a) Une expression donnée par Lucas a 94
comme entier. Pour les trois autres, 96 est l'entier. Trouvez ces quatre
expressions. Au besoin, composez un programme.
b) Par ailleurs, à l'époque, Lucas
n'avait pas trouvé quatre autres expressions. L'une a 3 comme entier. Les deux
autres ont 81 et la quatrième 82. Trouvez ces expressions.
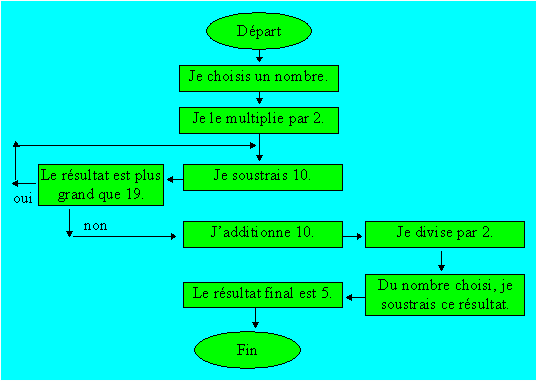
159. Un organigramme
Trouvez cinq nombres de départ qui vont donner
5 comme résultat final après avoir suivi le sens des flèches et fait les
opérations indiquées.
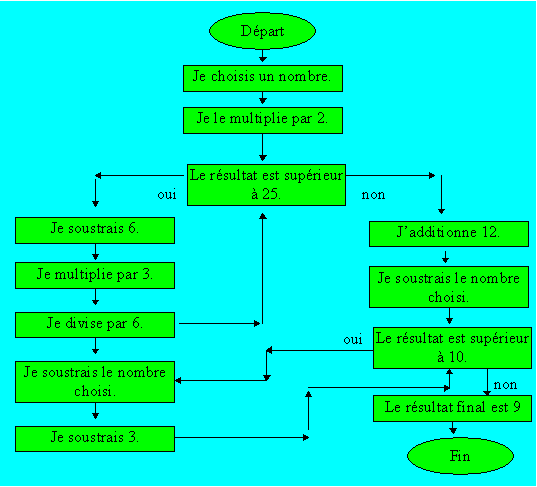
160. Un autre organigramme
Quel est le plus petit nombre de départ dont le
résultat final correspondant ne sera pas 9 ?
![]()
![]()