138. Vingt-cinq cases
Comme dans le problème précédent, pour chacune des grilles, trouvez un chemin où le cavalier parcourt le plus de cases possible à partir de 1.

139. Trente-six cases
Dans la grille ci-dessous, le cavalier part de 1 et doit parcourir toutes les cases pour s'arrêter à la case inférieure droite, laquelle est numérotée 36. Après plusieurs essais, Brenda n'a pas trouvé de solution. Guillaume affirme que le problème n'a pas de solution. Mais, il n'est pas capable de le démontrer.

143. Le cavalier continu
Dans la grille ci-après, un cavalier saute sur toute case munie d'un point. Un segment relie deux points consécutifs.

Dans une grille de même grandeur, indiquez un trajet où le cavalier doit atteindre 15 cases. Vous pouvez partir de n'importe laquelle case. Vous passez au plus une fois par case. Attention! Le trajet du cavalier ne doit jamais se couper.

144. Erreurs de transcription
Hélène a réussi à déplacer le cavalier dans une grille 6 ´ 6 en passant une fois sur chaque case. Au passage, elle a numéroté les cases à partir de la case 1 jusqu'à 36. Malheureusement, en copiant les nombres, elle a écrit un mauvais numéro dans neuf cases.

145. Le taquin
Cent ans avant la création du cube de Rubik, soit en 1878, l'américain Sam Loyd (1841-1911) popularisa un jouet qui fit fureur à l'époque : le taquin. Une variante des règles du taquin consiste à placer 15 blocs numérotés de 1 à 15 sur une planche carrée. Les blocs de 1 à 13 sont placés dans l'ordre croissant ; tandis que le 14 et le 15 sont intervertis.

Le jeu consiste à déplacer successivement les blocs de façon à remettre en ordre le 14 et le 15 tout en conservant à la fin le bon ordre des autres numéros. Plusieurs personnes crurent avoir résolu l'énigme ; mais personne ne put se souvenir des mouvements effectués. En réalité, le problème est insoluble. D'ailleurs, la démonstration en a été faite.

Découpez 15 petits carrés congrus. Numérotez-les de 1 à 15. Dans chacun des cas, placez les carrés comme dans le tableau de gauche. Déplacez les pièces d'une case à une autre libre horizontalement ou verticalement afin d'obtenir le tableau de droite.

a)

146. Le caméléon
Ce solitaire a été inspiré par le taquin. Le caméléon est formé par un octogone étoilé qui comprend neuf cellules : quatre blanches et cinq noires.

Découpez huit jetons. Inscrivez sur chacun une lettre du mot CAMELEON. Placez les jetons au hasard sur les cellules des sommets de l'octogone. Le déplacement entre deux cellules noires se fait en suivant les lignes dans les deux sens ; tandis qu'entre deux cellules de couleurs différentes, il se fait dans le sens contraire des aiguilles d'une montre.

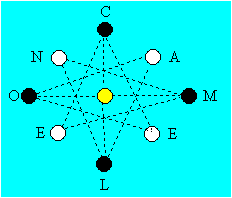
À la fin, chaque lettre doit être à sa place.

147. Le paradoxal tricolore
Le paradoxal tricolore est un autre solitaire inspiré du taquin. Il est formé par un dodécagone ayant 12 cellules sur le contour et quatre cellules intérieures. Sur le contour, il y a alternativement deux cases blanches et une noire.

Découpez 16 jetons : quatre gris numérotés 1, 2, 3 et 4 ; quatre noirs numérotés 1, 4, 7 et 10 ; huit blancs numérotés 2, 3, 5, 6, 8, 9, 11 et 12. Retirez au hasard un jeton gris et placez les autres, chacun sur une cellule, toujours au hasard.

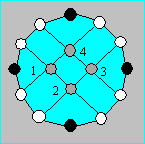
Vous déplacez un jeton sur une case vide en suivant les lignes. À la fin, il faut que chaque jeton gris se trouve à sa place et que les autres jetons se trouvent sur les cellules de même couleur en ordre numérique dans le sens de déplacement des aiguilles d'une montre.

148. Une somme chanceuse
Deux joueurs : Armande et Bertrand.

Chacun des deux joueurs choisit le nombre 1, 2 ou 3. Ensemble, les deux joueurs indiquent le nombre choisi. Si la somme des deux nombres est paire, Armande gagne un point. Si elle est impaire, c'est Bertrand qui accumule un point. Le premier qui atteint 20 points est le gagnant.

Ce jeu est-il équitable ? En d'autres mots, est-ce que les deux joueurs ont une chance égale de gagner ?

149. Le cube de Rubik et ses rejetons
En 1878, Sam Loyd inventa une variante du taquin, appelée jeu du 14-15. Cette variante fit à l'époque beaucoup de bruit et connut un succès considérable aux États-Unis et en Europe. Cent ans plus tard, un autre jouet, le cube de Rubik, a connu une très grande popularité. Inventé par le hongrois Ernö Rubik, le cube s'est vendu à des millions d'exemplaires. Au Québec, le cube a connu ses heures de gloire dans les endroits publics, dans les foyers et ... dans les classes.

Ce qui est remarquable au sujet du cube de Rubik, c'est qu'il a provoqué une véritable explosion de création et qu'il a fait la promotion du loisir à caractère géométrique. De nombreux jouets, inspirés par le cube ou par son succès, ont vu le jour.

Outre le cube de poche ayant quatre facettes par face, le maxi-cube avec 16 facettes par face et les nombreuses variantes du cube lui-même comme le carré magique, citons cinq modèles.

a) Le serpent de Rubik
Le matériel consiste en une chaîne de pyramides accolées mais qui peuvent pivoter. Le but du jeu est de produire des figures spatiales. Ce jeu se rapproche du tangram.

b) Le chaînon manquant
Le matériel consiste en un parallélépipède dont chacune des faces en hauteur contient quatre sections mobiles verticalement et horizontalement. Le but est de remettre sur chaque face les chaînons de même couleur en les reliant l'un à l'autre.

c) La pyramide
Chacune des faces d'un tétraèdre contient neuf triangles équilatéraux. Trois sections sont mobiles à partir de chacune des faces. Le but est de rendre chaque face de couleur uniforme.

d) Les anneaux hongrois
Deux anneaux se touchent en deux intersections. Trente-huit billes peuvent circuler dans les anneaux : neuf rouges, neuf jaunes, dix noires et dix bleues. Le but est de réaliser les configurations qu'on a d'abord établies.

e) La tour de Babylone
C'est une tour composée de six colonnes. Six billes de même couleur, mais dégradée, apparaissent sur chaque colonne. Les billes se déplacent horizontalement et verticalement. Le but est de placer les billes de même couleur sur chaque colonne selon le contraste normal.

150. Le tic-tac-toe
Le tic-tac-toe est un jeu très populaire. À peu près tout le monde, un jour ou l'autre, a aligné des croix et des ronds dans une grille 3 ´ 3 afin de compléter une rangée. Une analyse des différents mouvements permet de prévoir de quelle façon se déroulera l'issue du jeu. L'intérêt du tic-tac-toe réside dans les stratégies qui peuvent être développées. Il s'avère intéressant d'expérimenter des variantes au tic-tac-toe ou d'en inventer. Voici quelques exemples :

a) Qui perd gagne
Le but du jeu est d'éviter d'occuper trois cases en ligne droite. Le perdant est celui qui occupe le premier une rangée de trois cases.

b) Tic-tac-toe magique
Les deux joueurs se partagent des jetons numérotés de 1 à 9. L'un choisit les nombres pairs et l'autre les impairs. Le joueur qui a les nombres impairs commence. Le but est de compléter une rangée de trois nombres dont la somme est 15.

c) Une grille agrandie
On prend une grille carrée 4 × 4. On applique les mêmes règles que le tic-tac-toe classique. Après quelques essais, les joueurs remarqueront l'importance des cases centrales et se mettront sûrement d'accord pour modifier les règles concernant ces cases.

d) D'autres modèles
Tout en s'inspirant des principes de bases du tic-tac-toe, il est possible de modifier les règles de façon à rendre difficile une stratégie gagnante. Voici deux exemples de diagrammes pour lesquels des règles peuvent être précisées :

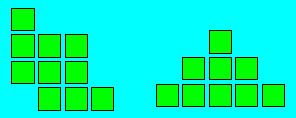
e) La marelle simple
La marelle simple est une version du tic-tac-toe. Le tableau se présente ainsi :

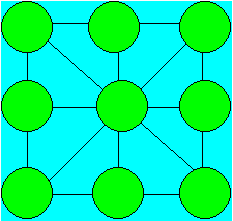
Chaque joueur a trois pions d'une même couleur. À tour de rôle, chacun place un pion sur une cellule du tableau. Quand les six pions sont posés, chaque joueur alternativement en déplace un sur une cellule voisine en suivant les droites. 

Le joueur qui, le premier, place ses trois pions sur une même rangée horizontale, verticale ou diagonale est le gagnant.

151. Master Mind
Ce problème est inspiré du Master Mind. Trois codes indiquant la couleur des fiches sont donnés dans l'ordre avec l'évaluation. L'étoile indique qu'une fiche de codage de cette rangée est de la bonne couleur et dans la bonne position. Le cercle indique qu'une fiche de codage de cette rangée est de la même couleur qu'une fiche du code mais dans une autre position.

1^e rangée : rouge noir jaune blanc     ¦ ¦

2^e rangée : bleu bleu vert vert            I I

3^e rangée : bleu rouge noir vert          ¦ ¦

Au moyen des informations contenues dans ces trois codes, déterminez la couleur des quatre fiches du code final.