49. Un carré incomplet
Complétez le carré ci-après de façon à obtenir la même somme dans chaque rangée horizontale, verticale et diagonale.

50. Magie alternative
Choisissez dans chaque case un nombre de sorte que la somme des nombres de chaque ligne, de chaque colonne et de chaque diagonale soit égale à 27.

51. Carrés premiers
On peut construire des carrés magiques en utilisant uniquement des nombres premiers. Voici deux exemples :

Formez deux carrés magiques constitués de neuf nombres premiers inférieurs à 300. Dans chacun des cas, les plus petits nombres sont :

a) 29, 41 et 53

b) 31, 37 et 43

52. Octomagie
Dans les cases du carré, placez les nombres de 1 à 8 pris deux fois de sorte que la somme des nombres dans chaque ligne, chaque colonne et chaque diagonale soit égale à 18.

53. La magie de 1982
Complétez la grille avec les chiffres 1, 9, 8 et 2. Il faut arriver à une somme de 20 dans chaque ligne et dans chaque colonne.

54. Vingt-cinq cases
Chacun des carrés suivants doit contenir les nombres de 1 à 25. De plus, la somme des nombres dans chaque rangée horizontale, verticale et diagonale doit être 65.

Complétez les deux carrés.

55. Déplacements
Dans la grille, intervertissez trois couples de deux nombres de façon à ce que la somme des nombres de chaque ligne, de chaque colonne et de chacune des deux diagonales soit égale à 65. Les déplacements se font successivement dans la première, la deuxième et la quatrième ligne.

56. Quarante-neuf cases
Examinez attentivement la disposition des nombres de 38 à 52. Placez dans la grille les nombres de 4 à 37. La somme des nombres dans chaque rangée horizontale, verticale et diagonale doit être 196.

57. Soixante-quatre cases
Placez dans la grille les nombres de 32 à 64 de sorte que la somme des nombres dans chaque rangée horizontale et dans chaque rangée verticale soit égale à 260. Le passage d'une case à une autre ayant deux numéros consécutifs se fait à la façon du cavalier aux échecs, soit en L.

58. Un rapport incomplet
Martine qui enseigne les mathématiques doit remettre au secrétariat de son école les résultats de trois élèves pour chacun des trois trimestres de l'année. Elle fait parvenir le rapport suivant :

La secrétaire fut étonnée du fait qu'il manquait des résultats. Elle communiqua avec Martine. Celle-ci lui répondit :

- Je ne me souviens plus des résultats. Mais, je me rappelle que la somme des notes pour chaque élève, pour chaque trimestre et même pour chacune des deux diagonales est la même partout.

Trouvez les résultats qui manquent.

59. Des théorèmes
a) Dans un carré magique d'ordre 3, le terme du milieu est toujours le tiers de la densité du carré magique. On sait que la densité est la somme de chaque rangée horizontale, verticale et diagonale.

Démontrez cette proposition.

b) Dans un carré magique d'ordre 3, la somme des carrés des éléments de la première rangée horizontale est égale à la somme des carrés des éléments de la troisième rangée horizontale.

Par exemple, on peut écrire : 17² + 8² + 14² = 12² + 18² + 9² quand on considère le carré ci-dessous.

Démontrez cette proposition. Un conseil : Construisez d'abord un carré magique avec des lettres. Par exemple, le centre pourrait être k.

c) Formulez une proposition similaire par rapport aux colonnes et vérifiez votre proposition.

60. Un système d'équations
Résolvez le système d'équations suivant si a = 5, b = 12 et c = 13.

a + b + c = d + e + f

a² + b² + c² = d² + e² + f²

61. Un triangle dense
Un triangle est dense si la somme des nombres est la même dans chaque rangée de trois cases. Dans le triangle, inscrivez les nombres 1, 2, 5, 6, 7, 10 et 11 pour que la somme soit 18 dans chaque rangée.

62. Un autre triangle dense
Formez un triangle dense avec les nombres 6, 7, 9, 10, 11, 13 et 14.

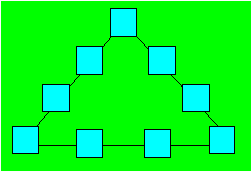
63. Un triangle quadruplé
Placez les nombres 1, 3, 5, 7, 9, 11, 13, 15 et 17 dans les cases vides pour que la somme des nombres sur chaque côté du triangle soit égale à 34. Il existe quatre configurations.

64. Distractions
Sur chaque côté d'un triangle, on fait la somme des sommets ; puis, on retranche le nombre du milieu. Si on obtient le même résultat sur chaque côté, on dit que le triangle est distrait. Le triangle ci-après est distrait, car 6 - 8 + 10 = 8, 10 - 7 + 5 = 8 et 5 - 3 + 6 = 8.

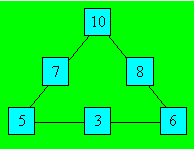
a) Placez sur ce triangle distrait les nombres 2, 4, 5, 8, 9 et 11. Le résultat sur chaque côté doit être 15.

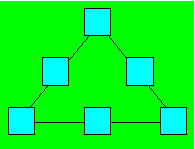
b) Construisez un triangle distrait dont le résultat est 0 en disposant chacun des nombres de 1 à 6.

c) Construisez un triangle distrait dont le résultat est le plus grand possible en disposant chacun des nombres de 1 à 6 dans les cases.

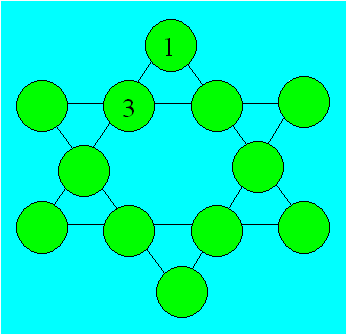
65. Étoile magique
Placez les nombres impairs de 5 à 23 dans les cercles. La somme des nombres de quatre cercles reliés par une même droite doit être partout égale à 48. Il existe quatre façons de distribuer les nombres.

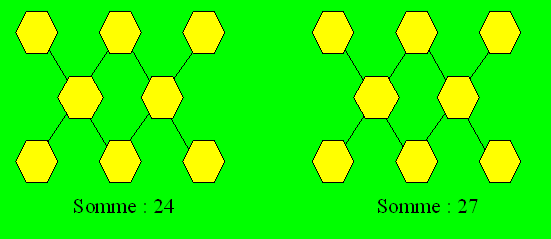
66. Un khi magique
Placez les nombres de 5 à 12 dans les cellules vides de chaque figure. La somme des nombres des cellules reliées par une même droite est donnée dans chaque cas.

67. Un serpent
Placez les nombres de 1 à 11 chacun une seule fois de sorte que la somme des nombres sur chaque rangée de trois cases adjacentes soit égale à 20.

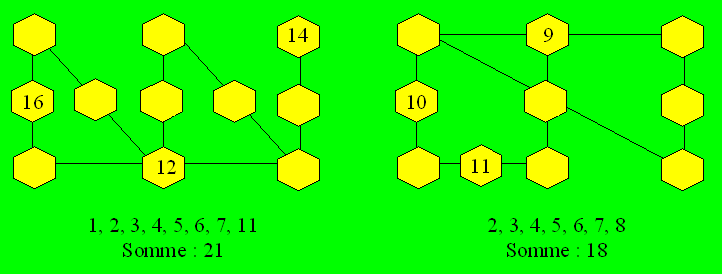
68. Cercles additifs
Dans les cellules, placez les nombres donnés sous chaque grille. La somme des nombres de trois cellules reliées par une droite est aussi indiquée. Des nombres sont déjà placés.

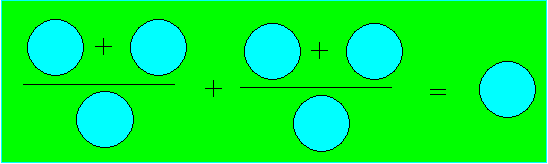
69. Addition magique
Placez dans les cercles les nombres de 1 à 7 chacun une seule fois de façon à ce que l'égalité soit vérifiée.

70. Un pavage magique
La figure suivante est étonnante. Une seule configuration existe. Elle a été découverte indépendamment par deux chercheurs : l'américain Clifford W. Adams en 1957 et l'anglais T. Vickers en 1958. Adams y avait consacré 47 ans de travail par temps libre quand il trouva la configuration qu'il égara. Il reprit alors sa recherche et trouva sa feuille de papier au bout de cinq ans. C'était en décembre 1962. Il expédia sa configuration à Martin Gardner qui en fit écho dans un article du Scientific American en août 1963. Antérieurement, Vickers avait publié la configuration dans Mathematical Gazette de décembre 1958.

a) Placez dans les cellules les nombres de 1 à 15 chacun une seule fois. La somme doit être 38 dans chaque rangée de trois, de quatre ou de cinq cellules alignées et adjacentes. Il y a, en tout, 15 rangées : six de trois cellules, six de quatre cellules et trois de cinq cellules.

b) Démontrez que la somme donnée, soit 38, est unique pour ce pavage, c'est-à-dire qu'aucune autre somme ne peut engendrer de configuration.

71. Sommes différentes
Dans ce pavage, placez les nombres de 1 à 15 de telle manière que la somme des éléments de chaque rangée de trois cellules est 22, que cette somme est 42 dans chaque rangée de quatre cellules et 62 dans chaque rangée de cinq cellules.

72. En amande
Combien y a-t-il de façons de lire AMANDE en suivant tous les chemins possibles ?

A

73. Un tablier
Sur un tablier carré de 16 cases, vous placez quatre jetons rouges, quatre bleus, quatre verts et quatre noirs. Aucun jeton d'une même couleur ne doit apparaître dans une rangée horizontale, verticale ou diagonale de quatre pièces.

Combien y a-t-il de dispositions différentes possibles ?

74. Un carré latin partagé
Dans le carré, ajoutez trois 1, trois 9, trois 8 et trois 2. Chaque ligne, chaque colonne et chacune des deux diagonales doivent avoir un chiffre différent.

75. En croix
Complétez la grille carrée avec des nombres de 1 à 6 de telle manière qu'un nombre apparaît une seule fois dans chaque rangée horizontale et verticale.

76. Une grille croisée
Dans la grille, placez sept 1, sept 2, sept 3, sept 4, sept 5, sept 6. Chaque ligne, chaque colonne et chacune des deux diagonales ne doivent pas contenir de nombres identiques.

77. Mathématique
Julie écrit le mot MATHÉMATIQUE en le répétant sans cesse. Elle est en train d'écrire sa millième lettre.

Quelle est cette lettre ?

78. Tout pour 125
Placez un des chiffres 1, 2, ou 5 par case de façon à ce qu’on puisse lire 125 sept fois dans la grille. Ce nombre peut être lu de gauche à droite, de haut en bas ou en diagonale.

79. Des chiffres à la suite
À partir des chiffres de cette grille, on peut former des nombres de quatre chiffres en se déplaçant en ligne droite ou à angle droit horizontalement et verticalement dans n'importe lequel sens. Ainsi, on peut lire 3494, 4276, 3921.

a) Déterminez le plus petit nombre de quatre chiffres de la grille qui peut être lu.

b) Déterminez le plus grand nombre de quatre chiffres.