96. Triangles et carrés
On a tracé la figure ci-après.

a) Trouvez le nombre de triangles de toute grandeur.

b) Trouvez le nombre de carrés de toute grandeur.

97. Carrés de 36 cases
On a tracé la grille ci-après.

Dans cette grille, trouvez le nombre de carrés

a) 2 × 2

b) 3 × 3

c) 4 × 4

d) 5 × 5

e) de toute grandeur

98. Carrés de 49 cases
On a tracé la grille ci-après.

Dans cette grille, trouvez le nombre de carrés

a) 2 × 2

b) 3 × 3

c) 4 × 4

d) 5 × 5

e) 6 × 6

f) de toute grandeur

99. Carrés de 64 cases
Dans une grille carrée 8 × 8, combien peut-on compter de carrés de toute grandeur ?

100. Quadrillage géant
Mathieu dessine une grille carrée 100 × 100. Combien peut-il compter de carrés de toute grandeur dans cette grille ?

En respectant ces conditions, trouvez le maximum de carrés congrus qui peuvent être construits dans cette figure de points.

105. Fantaisies chiffrées
Un fantaisiste a décidé d'écrire les chiffres et les opérations au moyen de segments congrus. Par exemple, on peut écrire 3 avec 13 segments en faisant 12 ¸ 4 = 3.

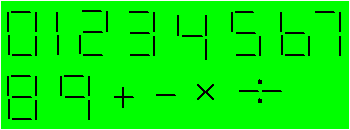
En utilisant un ou des signes d'addition, de soustraction, de multiplication ou de division au besoin, écrivez 16 successivement au moyen de :

· 7 segments

· 8 segments

· 9 segments

· 10 segments

· 11 segments

· 12 segments

· 13 segments

· 14 segments

· 15 segments

On peut utiliser l’élévation à une puissance.

106. D'autres fantaisies chiffrées
Les chiffres et les opérations sont écrits au moyen de segments comme dans le problème précédent. Le signe = exige deux segments.

Dans chacun des cas, rétablissez l'égalité.

107. Piste circulaire
Une piste circulaire a un diamètre de 500 mètres. Cependant, Nathalie a dû acheter un terrain carré.

Quelle est l'aire de terrain nécessaire pour construire une telle piste ?

108. Un enclos
Martin a un champ rectangulaire de 20 mètres par 70 mètres.

Il désire construire un enclos triangulaire ayant un angle droit et dont un côté mesure 20 mètres. Chaque côté est exprimé en nombre entier de mètres.

Déterminez les mesures des autres côtés de l'enclos.

109. Découpage
Découpez 14 carrés : quatre carrés 2 ´ 2, six carrés 4 ´ 4 et quatre carrés 6 ´ 6.

Accolez les 14 carrés de façon à former un grand carré.

110. Avec des diagonales
En traçant uniquement des diagonales dans les petits carrés, partagez le carré suivant en cinq carrés congrus et douze triangles congrus. Les 17 figures n'empiètent pas les unes sur les autres et couvrent tout le carré.

111. Une planche de bois
André a une planche de bois qui mesure 60 centimètres par 160 centimètres.

Il veut utiliser cette planche pour recouvrir le fond d'une case, dont la longueur est de 120 centimètres et la largeur de 80 centimètres. Il ne doit faire qu'un seul trait de scie.

Aidez André à résoudre ce problème.

112. À trait continu
Partagez ce carré au moyen de cinq lignes droites sans lever le crayon de façon à obtenir 12 parties.

113. D'un à l'autre
Partagez ce carré en neuf carrés congrus et en quatre triangles congrus.

114. Neuf droites
Le cercle ci-dessous a été divisé en un maximum de huit parties au moyen de quatre segments de droite sans lever le crayon et en touchant toujours à la circonférence aux extrémités.

En respectant les règles données, trouvez le plus grand nombre de parties qu'on peut obtenir en partageant un cercle successivement au moyen de :

a) cinq segments.

b) six segments.

c) sept segments.

d) n segments.

115. Champs rectangulaires
a) Partagez un champ rectangulaire de 15 mètres par 3 mètres en neuf rectangles ou carrés respectivement d'aire : 1, 2, 3, 4, 5, 6, 7, 8 et 9 mètres carrés.

b) Partagez un champ rectangulaire de 9 mètres par 5 mètres en neuf rectangles ou carrés ayant les mêmes aires que ci-dessus.

116. Un potager
Marie-Anna a un potager de 100 mètres par 60 mètres. Elle le partage entre ses quatre enfants : Armande, Bertrand, Réjeanne et Normand.

Réjeanne a le double du terrain d'Armande ; Normand a le triple du terrain d'Armande et le double de celui de Bertrand.

Partagez ce terrain de façon à utiliser seulement deux rangées de clôtures.

117. Terrain clôturé
Une fermière est prête à vendre 896 mètres carrés de terrain à Maténix à la condition que celui-ci place une clôture autour du terrain. Maténix propose à la fermière les mesures du terrain qui lui permettent d'avoir le moins long possible de clôture.

Quelles sont les mesures du terrain, exprimées en nombres entiers ?

Quel est le périmètre de l'île ?

123. Arrêts temporaires
Cette figure contient neuf étapes : AB, BC, AD, CF, BD, BE, BF, DE et EF.

René part de A et désire se rendre à F en cinq étapes différentes. Trouvez les trajets possibles.

124. Silhouettes
Tracez cinq triangles équilatéraux congrus sur du carton ou du papier fort. Découpez-les. Assemblez les pièces en les juxtaposant côté à côté. Formez le plus grand nombre de figures différentes. Par exemple, avec quatre triangles équilatéraux congrus, on peut former trois figures. Les voici :

Découvrez toutes les figures possibles et différentes en utilisant cinq pièces. Une figure qui coïncide avec une autre à la suite d'une rotation ou d'une réflexion est considérée comme identique.

125. En orbite
Encerclez les nombres de 3 en 3 en commençant par 1. Quand vous rencontrez une case encerclée, vous ne la comptez pas. À la fin, il restera une seule case dont le nombre n'est pas encerclé. Quel est ce nombre ?