Polygone formé de cinq côtés. On peut obtenir un pentagone régulier en joignant de deux en deux les sommets d’un décagone régulier. Le pentagone régulier est l'objet de dissection. Il peut être découpé en un nombre minimum n de pièces qui sont alors assemblées pour former chacune des figures indiquées. Sauf les croix, les polygones sont réguliers.

Il y a six façons de joindre les sommets d'un pentagone de façon continue pour obtenir une courbe fermée en passant une seule fois par chaque sommet. Les voici :

En traçant successivement les diagonales d'un pentagone régulier comme dans la cinquième figure, on peut reproduire indéfiniment des pentagones réguliers toujours plus petits. 

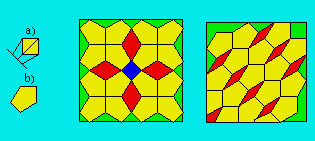
Avec des pentagones non réguliers, on peut produire des mosaïques. Pour obtenir une pièce pentagonale, on trace d’abord un carré comme en a. On trace une diagonale qu’on prolonge au-delà du carré. On trace une perpendiculaire à cette diagonale. On trace deux droites partant à égale distance du pied de la diagonale prolongée jusqu'à un sommet du carré. On obtient la pièce en b. On assemble un certain nombre de ces pièces et, au besoin, on complète avec d’autres figures. 

Voici deux exemples de mosaïques :

Le tableau suivant contient les 10 plus petits nombres pour chacune des classes de nombres figurés reliés au pentagone. La dimension D est donnée pour chaque classe.

© Charles-É. Jean

Index : P