| Roues
Certains problèmes peuvent être résolus en faisant un
choix parmi plusieurs stratégies. Le problème suivant en est un exemple puisqu’on
peut le résoudre par au moins 12 stratégies.
Problème. Julie a compté 42 roues dans un stationnement
où il y a des automobiles et des bicyclettes. Combien y a-t-il d’automobiles
et de bicyclettes, s'il y a en tout 15 véhicules ?
Démarche. Voici 12 stratégies :
Stratégie 1. Écrire une équation.
³ Stratégie d’application
Soit a le nombre d’automobiles et b le nombre de bicyclettes, on
peut écrire 4a + 2b = 42 et a + b = 15. La
résolution du système d’équations donne : a = 6 et b =
9. D’où, il y a 6 automobiles et 9 bicyclettes.
Stratégie 2. Faire une fausse supposition.
³
Stratégie d’enchaînement logique
On suppose que le nombre de bicyclettes est de 3 et que le nombre d’automobiles
est de 12. Cela donnerait 54 roues. Il y a 12 roues de trop. Quand on retranche
de 1 le nombre d’automobiles, le nombre de bicyclettes doit augmenter de 1 :
ce qui fait une différence de 2 roues. Comme il y a 12 roues de trop, on ajoute
6 bicyclettes et on retranche 6 automobiles : ce qui donne 6 automobiles et
9 bicyclettes.
Stratégie 3. Partir de l’unité.
³
Stratégie d’enchaînement logique
On pose que le nombre d’automobiles est l. Pour avoir 42 roues, il faudrait 19
bicyclettes : ce qui donnerait 20 véhicules. Quand on augmente de 1 le
nombre d’automobiles, le nombre de bicyclettes doit diminuer de 2. Pour
arriver à 15 véhicules, il faut une diminution de 5 véhicules. D’où, on
fait une augmentation de 5 automobiles et une diminution de 10
bicyclettes : ce qui donne 6 automobiles et 9 bicyclettes.
Stratégie 4. Procéder par déduction.
³
Stratégie d’enchaînement logique
Une automobile et une bicyclette ont 6 roues. Si les deux nombres cherchés sont
égaux, on peut diviser 42 par 6, ce qui donne 7. On aurait alors 14 véhicules.
Le nombre de roues d’une automobile est le double de celui d’une bicyclette.
D’où, on retranche une automobile et on ajoute deux bicyclettes : ce qui
donne 6 automobiles et 9 bicyclettes.
Stratégie 5. Procéder par étapes concourantes.
³
Stratégie d’enchaînement logique
On divise 42 par 15 : ce qui donne 2,8 roues. D’où, il y a plus de
bicyclettes que d’automobiles. On divise 42 par 4 : ce qui donne 10,5
véhicules. D'où, il y a un nombre impair de bicyclettes. On combine ces deux
conclusions. Il peut y avoir 13 bicyclettes et 2 automobiles : 34
roues ; 11 bicyclettes et 4 automobiles : 38 roues ; 9
bicyclettes et 6 automobiles : 42 roues. Il y a en tout 6 automobiles et 9
bicyclettes.
Stratégie 6. Simplifier les données.
³
Stratégie d’enchaînement logique
Comme 42 et 15 sont tous deux divisibles par 3, on cherche la solution pour 14
(42 ÷ 3) roues et pour 5 (15 ÷ 3) véhicules. On trouve 2 automobiles et 3 bicyclettes. On multiplie ces
résultats par 3 pour obtenir 6 automobiles et 9 bicyclettes.
Stratégie 7. Procéder par recherche systématique.
³
Stratégie de recherche
Il y a au plus 10 automobiles, car 42 ÷ 4 = 10,5.
On
essaie avec 10 automobiles. Pour 5 bicyclettes, cela donne 50 roues.
On essaie
avec 9 automobiles. Pour 6 bicyclettes, cela donne 48 roues.
On essaie avec 8
automobiles. Pour 7 bicyclettes, cela donne 46 roues.
On essaie avec 7
automobiles. Pour 8 bicyclettes, cela donne 44 roues.
On essaie avec 6
automobiles. Pour 9 bicyclettes, cela donne 42 roues.
Stratégie 8. Rechercher les combinaisons.
³
Stratégie de recherche
Le nombre 42 n'est pas divisible par 4. D'où, il y a un nombre impair de
bicyclettes. Il y a 15 véhicules. Les combinaisons possibles (bicyclettes,
automobiles) sont : (1, 14), (3, 12), (5, 10), (7, 8), (9, 6), (11, 4),
(13, 2). La combinaison (9, 6) est retenue.
Stratégie 9. Rechercher une régularité.
³
Stratégie de recherche
S’il y a une bicyclette et 14 automobiles, on trouve 58 roues.
S’il y a 2 bicyclettes et 13 automobiles, on trouve 56 roues.
S’il y a 3 bicyclettes et 12 automobiles, on trouve 54 roues.
S’il y a 4 bicyclettes et 11 automobiles, on trouve 52 roues.
Quand le nombre de bicyclettes augmente de 1, le nombre de
roues augmente de 2. On soustrait 42 de 58. On divise le résultat par 2 :
ce qui donne 8. D’où, 9 bicyclettes et 6 automobiles.
Stratégie 10. Construire un graphique.
³
Stratégie de représentation
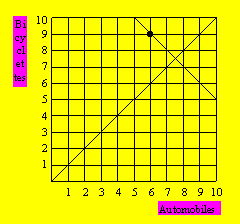
On place le nombre d’automobiles en abscisse et celui des bicyclettes en
ordonnée. On trace une première droite en supposant que le nombre d’automobiles
et de bicyclettes est le même. On trace une seconde droite qui correspond à 15
véhicules. Le point de rencontre est (7,5 , 7,5) : ce qui donnerait 45
roues. La solution est sur cette dernière droite vers le haut, car le nombre de
roues diminue en allant vers le haut, soit 6 automobiles et 9 bicyclettes.
Stratégie 11. Construire un tableau.
³
Stratégie de représentation
|
Automobiles |
1 |
2 |
3 |
4 |
5 |
6 |
|
Bicyclettes |
14 |
13 |
12 |
11 |
10 |
9 |
|
Roues |
32 |
34 |
36 |
38 |
40 |
42 |
Dans le tableau, on inscrit le nombre d’automobiles à
partir de 1. On déduit le nombre de bicyclettes du fait qu’il y a 15
véhicules. On calcule le nombre de roues : ce qui donne 6 automobiles et 9
bicyclettes.
Stratégie 12. Faire un dessin.
³
Stratégie de représentation
Le carré représente les automobiles et le cercle, les bicyclettes.

Or, il y a 15 véhicules. Il faut donc enlever 1 automobile
et ajouter 2 bicyclettes : ce qui donne 6 automobiles et 9 bicyclettes.
© Charles-É. Jean
Index
: R
|
![]()
![]()