u Rechercher une régularité.  – Stratégie de résolution de problèmes qui consiste à analyser chaque sous-ensemble de données, à comparer les résultats obtenus et à exprimer les liens qui existent entre les sous-ensembles. Cette régularité est trouvée par un raisonnement inductif. 

Dans certains cas, il est très difficile, voire impossible, d’affirmer que la régularité trouvée est constante. Toutefois, dans d’autres cas, on peut, par déduction, montrer que la régularité existe. 

La régularité peut être exprimée par une règle, par une formule ou par un ensemble d’expressions langagières ou mathématiques. Le tableau est souvent un outil précieux pour détecter la régularité. 

Cette stratégie en est une de recherche.

Problème 1. On dessine des figures géométriques selon le modèle suivant. Combien de carrés pourra-t-on trouver lorsque la base contient 15 carrés ?

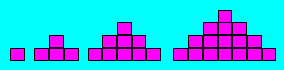
Démarche. On compte le nombre de carrés de chaque figure : 1^ère figure : 1 carré ;  2^e figure : 4 carrés ;  3^e figure : 9 carrés, 4^e figure : 16 carrés.

On constate que le nombre de carrés d’une figure est égal au carré du nombre correspondant au rang de la figure. La figure dont la base a 15 carrés sera la huitième. Elle contient 64 carrés.

Problème 2. Dans le tableau suivant, des nombres sont écrits selon un ordre logique. Quel serait le nombre placé à l’intersection de la huitième ligne et de la neuvième colonne ?

Démarche. On observe les liens qui existent entre les nombres. Les nombres placés horizontalement augmentent de 2 ; ceux placés verticalement augmentent successivement de 2, 3, 4. Ces derniers sont des nombres triangulaires. Le nombre placé à l’intersection de la 8^e ligne et de la 1^ère colonne sera 36, le huitième nombre triangulaire. Sur chaque ligne, il y a une différence de 16 entre le nombre de la 1^ère colonne et celui de la 9^e. Le 9^e nombre serait 17 (9 × 2 - 1). Sur chaque ligne, il y a une différence de 15 entre le 1^er nombre et le 9^e. 

D’où, le nombre cherché est 52, soit 36 + 16.

© Charles-É. Jean

Index : R