1^e  Produit de trois facteurs égaux. Le cube de 1,5 est 3,375. Lorsque la base du cube est un entier, le cube est dit parfait. Leonhard Euler (1707-1783) et Adrien Marie Legendre (1752-1833) ont démontré que la somme de deux cubes non nuls n'est jamais un cube.

n Le cube de la somme de deux nombres est égal au cube du premier, plus trois fois le produit du carré du premier nombre par le second, plus trois fois le produit du premier par le carré du second, plus le cube du second nombre. Par exemple, le cube de (8 + 5) est égal à : 512 + 960 + 600 + 125 = 2197.

n Si un nombre a deux chiffres, son cube est égal au cube des dizaines, plus trois fois le produit du carré des dizaines par les unités, plus trois fois le produit des dizaines par le carré des unités, plus le cube des unités. Par exemple, le cube de 85 est égal à : 512 000 + 96 000 + 6000 + 125 = 614 125. Si un nombre a plus de deux chiffres, on peut le décomposer en deux parties, l’une étant assimilée aux dizaines et l’autre aux unités. On applique alors l’algorithme donné. Par exemple, le cube de 119 (110 + 9) est égal à : 1 331 000 + 326 700 + 26 730 + 729 = 1 685 159.

n Quand on connaît le cube d’un entier n, on peut obtenir le cube de (n - 1) en soustrayant de (n³ - 1) le triple de (n² - n). Par exemple, on sait que 12³ = 1728, le cube de 11 est égal à : 1727 - 3(12² - 12) = 1331.

n Quand on connaît le cube d’un entier n, on peut obtenir le cube de (n + 1) en additionnant à (n³ + 1) le triple de (n² + n). Par exemple, on sait que 12³ = 1728, le cube de 11 est égal à : 1729 - 3(12² - 12) = 2197.

n La somme de n cubes impairs successifs à partir de 1 est un nombre triangulaire de rang (2n² - 1). Par exemple, 1³ + 3³ + 5³ + 7³ = 496 qui est un triangulaire de rang 31.

n La somme de n cubes pairs successifs à partir de 2³ est le double du carré d’un nombre hétéromèque de rang n(n + 1). Par exemple, 2³ + 4³ + 6³ + 8³ = 800 qui est égal à 2 × 20².

n La somme d’un cube de rang n et du carré du triangulaire de rang (n - 1) est égal au carré du nombre triangulaire de rang n. Par exemple, 5³ + 10² = 225 = 15². La base de la somme est égale à la somme des deux bases.

n Il existe six nombres qui sont égaux à la somme des chiffres de leur cube : 1, 8, 17, 18, 26 et 27 (Sloane, A046459). Par exemple, 26³ = 17576 et 1 + 7 + 5 + 7 + 6 = 26.

n Quand on élève au cube un nombre de la forme 3n, 3n + 1 ou 3n + 2, la somme des cubes de leurs chiffres est un nombre de la même forme. Par exemple, 29 est de la forme 3n + 2. La somme des cubes de ses chiffres est 2³ + 9³ = 737 ; ce nombre est de la forme 3n + 2. Si on soustrait le nombre de départ et la somme des cubes de ses chiffres, le résultat est un multiple de 3.

n Un nombre étant donné, on peut faire la somme des cubes de ses chiffres et répéter la même opération sur chacun des résultats obtenus. Par exemple, si le premier terme est 41, le deuxième sera 4³ + 1³ = 65, le troisième 6³ + 5³ = 341 et ainsi de suite.

Dans ce tableau, on constate :
1. Lorsque le nombre initial est de la forme 3n, la séquence s’arrête à 153.
2. Lorsque le nombre initial est de la forme 3n + 1, la séquence s’arrête à 370 ou se termine par un cycle.
3. Lorsque le nombre initial est de la forme 3n + 2, la séquence s’arrête à 371.

Les nombres 153, 370 et 371 sont des nombres narcissiques. Le carré magique suivant qui a été établi sur le modèle du numéro 175 de l’index de Frénicle a des propriétés par rapport aux cubes.

On peut écrire : 6 + 8 + 42 + 44 = 2 + 14 + 36 + 48 = 100 et 6³ + 8³ + 42³ + 44³ = 2³ + 14³ +36³ + 48³ = 160 000. De plus, la somme des cubes des huit éléments des deux diagonales est égale à la somme des cubes des huit éléments apparaissant en périphérie en excluant les coins. On a 49³ + 37³ + 13³ + 1³ + 7³ + 9³ + 41³ + 43³ = 320 000 et 6³ + 2³ + 14³ + 42³ + 44³ + 48³ + 36³ + 8³ = 320 000.

2^e  Hexaèdre régulier dont les six faces sont des carrés. Le cube a huit sommets et douze arêtes. Le dé le plus couramment utilisé est en forme de cube. Le patron nécessaire pour réaliser un cube peut prendre 11 formes, qui sont autant d'hexominos différents :

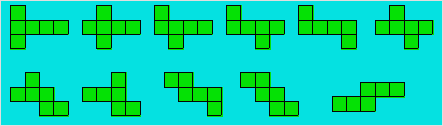
Il est impossible de décomposer un cube en un nombre fini de cubes tous non congruents. Le nombre maximum de cubes de même volume qui peuvent être mis en contact avec un autre cube est 14. Trois bandes sont suffisantes pour natter un cube. La duplication du cube est un problème célèbre. Le tableau suivant contient les 10 plus petits nombres pour chacune des classes de nombres figurés reliés au cube. La dimension D est donnée pour chaque classe.

Les termes relatifs au cube mentionnés dans ce dictionnaire, y compris certains treillis, sont :

3^e Base de certains solitaires comme ceux mentionnés ci-dessous :

© Charles-É. Jean 

Index : C

Voir aussi Cube dans l'Aide-mémoire.