u Rechercher une règle. – Stratégie de résolution de problèmes qui consiste à trouver une opération, un ensemble d’opérations ou un procédé à partir desquels les données sont appliquées. Cette règle, quand elle existe, est vraie indépendamment des données. L’élève peut trouver une règle par ses propres moyens ou par une recherche dans les manuels ou ailleurs. 

Pour trouver une règle, il faut généralement étudier un ensemble de situations et tirer une conclusion générale par un raisonnement déductif. Une règle peut être exprimée par une proposition ou une formule. Mais, elle peut être constituée d’un ensemble d’expressions langagières ou mathématiques. 

Cette stratégie en est une de recherche.

Problème 1. Combien y a-t-il de termes dans la suite : 7, 10, 13, 16, 19, .... 1000 ?

Démarche. On ramène chaque terme à son rang.
(10 - 7)/3 + 1 = 2 et 10 est le 2^e terme.
(13 - 7)/3 + 1 = 3 et 13 est le 3^e terme.
(16 - 7)/3 + 1 = 4 et 16 est le 4^e terme.
(19 - 7)/3 + 1 = 5 et 19 est le 5^e terme.

La règle qui se dégage est : « Pour trouver le rang d’un terme, on soustrait le premier terme du dernier. On divise cette différence par la raison de la suite. On additionne l’unité à ce quotient. ». D’où, (1000 - 7)/3 + 1 = 332 et 1000 est le 332^e terme. Il y a 332 termes dans cette suite.

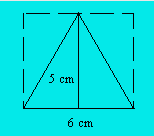
Problème 2. Trouvez l’aire d’un triangle isocèle dont la base est six centimètres et la hauteur cinq centimètres.

Démarche. L’élève ne connaît pas la formule de l’aire d’un triangle isocèle. Il trace le triangle en respectant les mesures données. Il élève deux perpendiculaires aux sommets du triangle à la base ; puis, au sommet supérieur, une parallèle à la base. Il forme ainsi un grand rectangle. Il se rend compte que les côtés du triangle isocèle, excepté la base, sont les diagonales de deux rectangles congruents. Il conclut que l’aire d’un triangle isocèle est le demi-produit de la mesure de la base et de celle de la hauteur. L’aire du triangle isocèle est de (5 × 6)/2 = 15 centimètres carrés.

© Charles-É. Jean

Index : R