u Construire des modèles. – Stratégie de résolution de problèmes qui consiste à représenter la situation en des formes réduites, à traiter chacune des formes, à analyser les relations qui existent entre elles et à induire pour aboutir au résultat. Cette stratégie peut permettre d’observer des régularités. Elle en est une de représentation. 

Problème 1. Un cercle étant donné, tracez 10 lignes droites dont les extrémités touchent au cercle. Vous devez obtenir le plus grand nombre de parties. Combien de parties pouvez-vous obtenir ?

Démarche. Voici ce qui se passe quand on trace les quatre premières droites :

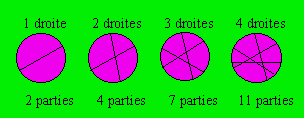
On remarque qu’il y a une augmentation de deux parties pour le deuxième cercle par rapport au premier, une augmentation de trois parties pour le troisième cercle par rapport au deuxième et une augmentation de 4 parties pour le quatrième cercle par rapport au troisième. On peut exprimer cela ainsi : 1^er cercle : 2 ; 2^e cercle : 2 + 2 ; 3^e cercle : 2 + 2 + 3 ; 4^e cercle : 2 + 2 + 3 + 4.

Ainsi, 2 + (2 + 3 + 4 + .... + 10 + 11 + 12) = ...... Le 12^e cercle contient 79 parties.

D’après cette régularité, on peut formuler les deux propositions suivantes qui expriment d’ailleurs la même situation :

1. Dans un cercle, le nombre de parties est égal à la somme du nombre de droites et le nombre de parties du cercle précédent.

2. D’un cercle à l’autre, le nombre de parties augmente du nombre correspondant au rang de la dernière droite tracée.

On peut exprimer cette régularité par une formule algébrique : Soit m le nombre de parties et n le nombre de cercles, alors m = (n² + n + 2)/2.

Problème 2. Monsieur Lafeuille est fier de son verger. La première année, il a planté 12 pommiers. La deuxième année, il en a planté 20. La troisième année, il en a planté 30. La quatrième année, il en a planté 42. En continuant selon le même rythme, combien Monsieur Lafeuille a-t-il planté de pommiers la 10^e année ?

Démarche. On peut représenter les nombres donnés par un rectangle de points.

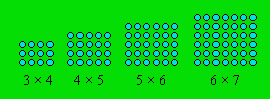
On voit que chaque nombre est le produit de deux entiers consécutifs. Le premier facteur du premier nombre est 3 ; celui du deuxième est 4 ; celui du troisième est 5 ; celui du quatrième est 6. Celui du 10^e nombre sera 12. Le nombre cherché est 12 × 13 = 156. Monsieur Lafeuille a planté 156 pommiers la 10^e année.

© Charles-É. Jean

Index : M