|
Le présent document vise à présenter les trois classes
principales de récréations
mathématiques et à les illustrer. Il a été élaboré pour ceux ou celles qui
veulent faire un survol rapide et avoir une idée plus précise du champ occupé
par les mathématiques récréatives. Cette classification s’attarde aux domaines de base des
mathématiques. Toutefois, il ne s’agit pas de produire une liste exhaustive
des objets récréatifs.
Partie 1. Récréations arithmétiques
|
"Les nombres sont pour nous
de vieilles connaissances. Nous avons grandi en leur compagnie et nous
les rencontrons tous les jours." C. Stanley Ogilvy |
Depuis que l’homme a inventé les nombres, ces derniers ont
pris une place importante dans la vie de tous les jours. Les conversations et
les travaux à un moment ou l’autre intègrent les nombres et leur concept.
Certains nombres ont la réputation d’être sans écart de conduite et
inspirent plutôt la cohésion et la bonne entente tandis que d’autres
semblent se moquer du bon sens. Aussi, avec les nombres s’est rapidement
développé un ensemble de problèmes qui constituent une bonne partie de l’héritage
récréatif.
Les récréations arithmétiques
sont basées sur les propriétés des nombres et mettent en
évidence les relations qui existent entre eux. Comme l’arithmétique est
connue de tous et qu’elle offre une grande variété d’activités, une place
importante lui est accordée dans le domaine récréatif. Pour mieux cerner la
production, les récréations arithmétiques ont été subdivisées en trois
classes : combinatoires, cryptarithmiques et numériques. Pour chacune des
classes, on indique certains sujets qui y sont traités et on donne des exemples
de problèmes.
1.1 Récréations
combinatoires
Les récréations combinatoires
touchent aux situations qui visent à disposer des chiffres ou des
objets d’une façon définie en se basant sur des procédés de dénombrement.
Les treillis magiques
Les récréations qu’on
appelle magiques nécessitent des diagrammes de formes géométriques diverses
qui contiennent des cases ou cellules dans lesquelles on peut écrire des
nombres. Ces derniers doivent être disposés de façon qu’on retrouve
généralement une constante dans chacune des rangées. La constante provient de
certaines opérations, le plus souvent l’addition. Les récréations magiques
les plus connues sont celles qui ont trait aux carrés
magiques.
Problème 1.
Dans les cases, écrivez les nombres pairs de 10 à 26 de façon à obtenir
un carré magique c’est-à-dire que la somme des nombres doit être la
même dans chaque rangée horizontale, verticale et diagonale.
Les solutions sont données.
Des carrés magiques
peuvent être formés avec des nombres non nécessairement consécutifs ou
entiers. C’est ainsi qu’il existe des carrés magiques constitués de
fractions, de nombres premiers, de palindromes. À part les carrés, il existe
des rectangles magiques. Ceux-ci
négligent les diagonales et exigent une somme proportionnelle des lignes et des
colonnes.
Problème 2.
Dans le rectangle, placez les entiers de 1 à 12 de façon que la
somme soit 40 sur chaque ligne et de 24 dans chaque colonne. Les nombres 13,
14 et 15 sont en bonne position.
À part les carrés et les rectangles magiques, il existe un grand nombre de
formes de treillis qui peuvent devenir magiques, comme les cubes, les cercles,
les polygones et les étoiles. Les rangées coïncident parfois avec le contour
de figures géométriques et s’entrecroisent, si bien que certaines cellules
appartiennent à plus d’une rangée.
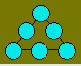
Problème 3 . Écrivez les
nombres de 1 à 6 dans les cellules du triangle. La somme sur chaque côté
doit être 11.
Les combinaisons
On peut créer de
nombreuses situations en faisant intervenir des objets qu’on combine en
appliquant parfois des opérations mathématiques.
Problème 4 .
Luc prend neuf jetons numérotés de 1 à 9. Combien y a-t-il de groupes
possibles de trois jetons dont la somme est 15 ?
D’autres
récréations sont connues comme la disposition de personnes autour d’une
table, les chaînes de dominos, les mains de cartes, les tournois. Les
probabilités, avec le triangle de
Pascal, sont également un centre d’intérêt remarquable pour les
récréations combinatoires.
1.2
Récréations
cryptarithmiques
|
"La
vraie culture ne peut exister sans une certaine teneur ludique." J.
Huizinga |
Les récréations
comportant des lettres qu’on peut traduire en chiffres étaient connues en
Chine et en Inde au Moyen Âge. On les appelle récréations cryptarithmiques.
Le cryptarithme
Un cryptarithme est
une récréation dans laquelle les lettres (ou les symboles) sont réunies en
une ou plusieurs opérations arithmétiques. À chaque lettre correspond un
chiffre différent. Par exemple, A = 7, B = 0, etc.
Problème 5. Déchiffrez ce
cryptarithme.
|
A P M Z
+ P M T Z
A S T A M |
L’alphamétique
L’alphamétique est
un cryptarithme dont les lettres forment des mots ou des phrases qui ont un
sens.
Problème 6.
Dans cette addition, quelle est la plus grande valeur de ONZE ?
L’astérithme
Une autre forme de
cryptarithme qu’on appelle l’astérithme existe depuis fort longtemps. Dans
ce problème, des astérisques indiquent l’existence de chiffres sans égard
à leur valeur respective. Seuls quelques chiffres sont donnés. Il s’agit de
retrouver ceux qui manquent.
Problème 7. Déchiffrez cet
astérithme qui est une multiplication au long.
|
4 * *
´ *
*
4 * * *
* * 4 *
4 * * * 4 |
1.3
Récréations
numériques
Les récréations
dites numériques sont reliées principalement à la théorie des nombres sous sa facture
ancienne. On y manipule les nombres en les faisant rebondir dans des sens
divers. Les dix chiffres interviennent assez souvent. Parfois, on exclut le 0.
On y utilise les propriétés élémentaires des nombres de même que des
opérations de base comme l’addition, la soustraction, la multiplication, la
division, l’extraction d’une racine et l’élévation à une puissance. Les
récréations numériques forment un immense domaine qui n’est pas encore
totalement exploré. C’est en faisant le tour de ce domaine qu’on découvre
la richesse des nombres et la puissance des calculs.
Le calendrier
Les récréations,
liées au temps, se concentrent en bonne partie autour du jour
de la semaine.
Problème 8.
Le 6 mai 1950, le feu transforme une partie de la ville de Rimouski en un
immense brasier. Quel jour de la semaine était-ce ?
Pour résoudre ce
problème, on a créé le calendrier
perpétuel et mis au point plusieurs formules. D’autres problèmes sont
relatifs à la date de Pâques et à la
disposition des nombres sur une feuille de calendrier.
L’âge
Le principe sur
lequel s’appuient les problèmes d’âges est que deux personnes vieillissent
en même temps.
Problème 9 .
Horace a trois ans de plus que Fabien. Dans six ans, Horace et Fabien auront
ensemble 47 ans. Quel est l’âge de chacun ?
L’argent
Dans la vie courante,
l’argent provoque de nombreuses situations qu’il est bon de rendre
amusantes.
Problème 10.
Jennifer a amassé 129 centimes répartis en 11 pièces de monnaie. Comment
peut-on former ce montant avec des pièces de 1, 5, 10 et 25 centimes ?
La partition d’un nombre
En utilisant des
chiffres donnés et des opérations, on peut représenter des nombres. Le
problème des 4 est bien connu.
Problème 11.
À l’aide d’opérations simples, écrivez 80 avec six 8.
Les fractions
Après les nombres
entiers, les fractions jouent un rôle important. Des cases peuvent être
disposées de telle façon qu’on peut lire une ou des fractions.
Problème 12.
Florence découpe sept jetons et les numérote de 3 à 9, sauf 7. Elle prend
quatre jetons dont la somme des numéros est 23 et les dépose sur le
tableau.
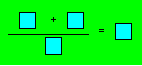
Disposez quatre
jetons pour que l’égalité soit vraie.
Les nombres croisés
À l’instar des
mots croisés, l’arithmétique amusante génère des nombres croisés. Les
indices sont parfois transparents, parfois complexes. On peut faire un clin d’œil
à l’algèbre comme dans cet exemple.
Problème 13.
Remplissez cette grille avec des chiffres à partir des définitions. On ne
connaît pas, cependant, les valeurs de a et de b.
A : a2
B : 75a
C : 51a
- 1
D : b2
E : 4a2
F : 68b
La calculatrice
Cet outil peut être
utilisé lorsque les calculs sont fastidieux ou comme prétexte à une
récréation.
Problème 14.
Ambroise possède une calculatrice qui affiche huit chiffres. Quel est le
plus grand carré que la calculatrice peut montrer ?
La magie arithmétique
Le calcul rapide, les
devinettes, les nombres pensés, les tours de carte sont des domaines qui
provoquent beaucoup de surprise et de mystification. Les tours sont basés sur
des opérations mathématiques parfois simples. Les magiciens savent, tout en
faisant des diversions, exploiter la puissance des liens entre les nombres et
les opérations.
Problème 15.
Prenez un nombre. Multipliez-le par 3. Additionnez 5. Soustrayez le nombre
choisi. Additionnez 13. Divisez par 2. Soustrayez le nombre choisi. Quel est
le résultat ?
Partie
2.
Récréations géométriques
|
"Il
est rare que les géomètres soient fins, et que les fins soient
géomètres." Pascal |
Dès le moment où l’homme
a eu besoin de construire des édifices, de partager des champs, il a dû
inventer la géométrie pratique. Puis, peu à peu, une géométrie théorique a
vu le jour. On envisageait alors les corps matériels au point de vue de leur
forme, de leur étendue et de leur position relative. Dans ce contexte, des
problèmes amusants apparurent. Ils permirent de percevoir une géométrie plus
fantaisiste basée sur l’union de la forme et du calcul. Les récréations géométriques
sont donc reliées principalement aux mesures et aux formes des
figures géométriques.
Le carrelage
Il s’agit de
constituer le plus souvent des carrés avec des pièces définies ou à trouver.
Problème 16.
Assemblez les pièces suivantes : un carré 6 ´
6, deux carrés 4 ´ 4, trois carrés 3
´ 3 et un certain nombre de carrés 1
´ 1. Vous
devez ainsi former un carré 10 ´
10. De combien
de carrés 1 ´ 1 a-t-on besoin ?
Le pavage
Assembler des
carreaux pour former un pavage ou un revêtement était un problème connu des
Pythagoriciens. Bien des formes géométriques peuvent être utilisées pour
recouvrir de façon indéfinie un plan sans vide et sans empiétement. Voici un
exemple de pavage :
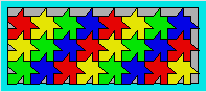
L’assemblage
Dans certains foyers,
les casse-tête sont un divertissement très populaire. En mathématiques, les
pièces peuvent être des figures géométriques remarquables.
Problème 17 .
Découpez 24 triangles équilatéraux de même grandeur. Coloriez 12 de ces
triangles en rouge et les 12 autres en bleu. Assemblez les triangles de
façon à former un hexagone régulier dont les carreaux sont
alternativement de couleur rouge et bleue.
La construction de figures
On peut construire
des figures avec une règle et un crayon. On peut le faire aussi avec des objets
comme les cure-dents ou les allumettes.
Problème 18.
Construisez trois carrés au moyen de 10 cure-dents.
L’alignement
Ces récréations
permettent de regrouper des objets qui sont mis en ordre, en classes ou à la
suite.
Problème 19 .
Joignez tous les A de cette figure par cinq lignes droites sans lever le
crayon. Toute ligne droite doit toucher à au moins trois A.
|
A |
A |
A |
A |
|
A |
B |
A |
B |
|
A |
A |
B |
A |
|
A |
A |
A |
A |
Les mesures
Ces récréations
considèrent l’étendue sous ses aspects de longueur, de surface et de volume.
De plus, elles touchent principalement aux propriétés et aux mesures de cette
étendue.
Problème 20.
Valère partage une pizza de façon que l’angle au centre soit de 60
degrés. Combien devra-t-il faire de traits de couteau ?
Le comptage des figures
Dans une grille
carrée 3 × 3, on peut compter 14 carrés de différentes grandeurs : neuf
carrés 1 ´ 1, quatre carrés 2
´ 2 et 1 carré 3 ´
3. Des triangles, des losanges,
des rectangles, des carrés peuvent être cachés dans certaines figures.
Problème 21.
Combien y a-t-il de carrés de toute grandeur dans une grille rectangulaire
3 ´ 5 ?
Le partage
Attribuer à chacun
exactement la même part n’est pas toujours facile. Comment diviser une tarte
en sept parties tout à fait égales ? Comment décomposer un carré en vingt
triangles égaux ? En respectant les règles élémentaires de la géométrie,
des partages astucieux peuvent se dégager.
Problème 22.
Un père avait de son vivant donné le quart de son terrain carré à l’aîné
de la famille. À sa mort, il légua par testament le reste du terrain à
ses quatre autres enfants. Mais, il fallait que chacun des quatre ait un
terrain de même forme et de même grandeur.
Partagez le
terrain.
Les illusions d’optique
Il existe plusieurs types d’illusions
d’optique qui proviennent de causes physiologiques ou psychologiques. Selon l’acuité
de nos yeux, il se peut que chaque jour des illusions visuelles nous arrivent
sans que nous les détections. L’illusion suivante est bien connue :
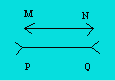
Les deux segments MN
et PQ sont d’égale longueur et pourtant …
La superficie
L’aire des carrés
et des rectangles peut être déterminée en partageant la figure en carrés
unitaires.
Problème 23. Alban a tracé le
rectangle suivant qui contient uniquement des carrés. Chaque carré unitaire
mesure un centimètre carré.
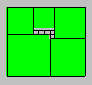
Trouvez l’aire de ce rectangle.
Les tracés de figures
En considérant des
points comme les sommets de figures géométriques connues ou inconnues, on peut
dessiner de nombreuses figures.
Problème 24. Boris a dessiné
12 points en un rectangle 3 ´ 4.
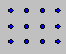
Combien peut-on
tracer de rectangles de toute grandeur si les points en sont les sommets ?
L’agencement de figures
Les allumettes
peuvent servir à écrire des chiffres romains, à dessiner des figures, à
représenter des nombres ou des lettres. Elles peuvent aussi servir à former
des figures.
Problème 25.
Cette figure nécessite trois allumettes sur le côté gauche ou droite.

Combien d’allumettes
seront nécessaires pour former cette figure ?
Le parcours d’un réseau
Reproduire les lignes
d’un dessin d’un point à un autre sans lever le crayon et sans passer plus
d’une fois sur une même ligne représente parfois un cauchemar, puisque
certains réseaux ne peuvent pas être parcourus. La clé du problème se trouve
dans le nombre de chemins qui passent par les points d’intersection. Si le
point de départ n’est pas donné, il faudra s’assurer que le point choisi
conduit à une solution.
Problème 26. Parmi les dessins
suivants, lequel ou lesquels peuvent être reproduits d’un seul
trait ?

Le triangle de Pythagore
Les anciens
Égyptiens, au moment où les mathématiques n’étaient pas encore tellement
développées, ne pouvaient pas déterminer la mesure de l’hypoténuse d’un
triangle rectangle en fonction des deux autres côtés. C’est en prenant une
corde et en y faisant 13 nœuds à égale intervalle qu’ils découvrirent la
relation 3, 4, 5 entre les côtés. Dans les récréations, on s’intéresse
principalement aux mesures en nombres entiers.
La topologie
La topologie utilise
les points, les lignes et les figures. Cependant, la topologie n’est pas
intéressée aux mesures elles-mêmes ; elle étudie plutôt les
propriétés des figures lorsque la forme varie. D’ailleurs, la théorie des
graphes est un support précieux dans la résolution de certaines récréations.
Le pliage de papier
Aussitôt que l’enfant
peut manipuler les objets avec une certaine aisance, il prend vite plaisir à
plier des feuilles de papier et à y découvrir des formes familières. Certains
pliages nécessitent des calculs ; d’autres paraissent curieux ou même
capricieux.
Les labyrinthes
Pour Euler, passer à
travers un labyrinthe, c’est partir du point prévu d’arrivée et de
chercher ainsi le chemin dans le sens inverse. Lorsqu’un créateur de
labyrinthes prévoit cette stratégie, il dissimule autant ou plus d’impasses
dans le parcours inverse et la stratégie échoue. Par ailleurs, certains
amateurs conviennent de prendre toujours le premier chemin à droite ou à
gauche jusqu’à ce qu’ils rencontrent une impasse ou un chemin déjà
parcouru. Dans ce cas, ils prennent alors le second chemin toujours du même
côté. Il existe, dans le plan, plusieurs formes de labyrinthes.
Partie
3.
Récréations logiques
|
" Chaque
vérité que je trouvais était une règle qui me servait après à en
trouver d’autres. " Descartes |
Il y a, dans la
solution de chaque récréation, une part de raisonnement. Cependant, il existe
des récréations qui sont essentiellement à base d’inférence, c’est-à-dire
que l’intelligence passe d’une vérité à une autre en raison du lien avec
la première qui a été jugée vraie. Ces récréations de nature logique
exigent peu de calculs et peu de transformations géométriques.
La logique ancienne
était une branche de la philosophie qui s’articulait autour du discours ; la
logique moderne, qui se veut algorithmique, se présente comme un système
scientifique du raisonnement. C’est dans ce contexte nouveau que les
récréations logiques se développent. Des outils précieux ont été inventés
par des logiciens qui désiraient symboliser des raisonnements.
Les énigmes
C’est souvent d’une
façon trompeuse ou piégée que les récréations de cette catégorie sont
présentées. On y trouve des questions d’astuce, des faux raisonnements, des
opérations illégales, des raisonnements faibles ou sans consistance, des
arguments faux déguisés en vérité, des arrangements d’idées en un ordre
vraisemblable mais non logique, des pièges qui sont parfois attirants, des
faussetés qu’il faut détecter. Souvent, le lecteur accrochera sur un détail
ou se laissera distraire par une incongruité mineure qui en cache une plus
grande. La subtilité de la question et l’art du ricochet amènent dans des
voies extérieures celui qui veut dénouer l’énigme. Le problème, même s’il
est posé avec des mots simples ou imagés, peut contenir des données
superflues.
Problème 27.
Deux mères et deux filles se rendent au cinéma. Le droit d’entrée d’une
personne est de 5 pistoles. Le commis réclame 15 pistoles. Pourtant, le
commis ne leur a donné aucune réduction et il ne s’est pas trompé.
Comment cela se fait-il ?
Les paradoxes
On croit une
proposition vraie et elle est fausse. On la croit fausse ; elle est vraie
ou simplement elle est contradictoire. Que peut-on penser de quelqu’un qui
dit : " Je suis menteur. " ; de l’autre qui écrit sur le mur d’un
corridor : " Il est interdit d’écrire sur ce mur. " ;
de l’autre enfin qui clame avec certitude : " Toutes les règles ont
des exceptions. " ?
Les cryptogrammes
La cryptographie est
une méthode d’écriture secrète au moyen de lettres, de signes ou de
chiffres. C’est l’art de composer des messages secrets qui sont
intelligibles seulement pour ceux qui connaissent la clé ou qui la découvrent.
Problème 28.
Déchiffrez ce message dans lequel les lettres sont toutes décalées d’un
même rang.
KF EFDPVWSF MF
DPEF
Les récréations d’affectation
Dans ces
récréations, à la manière d’un casse-tête, les pièces sont des
propositions en désordre. Chaque proposition doit être juxtaposée à une ou l’autre
pour aboutir à un tout cohérent. Édouard Lucas considère ces récréations
comme faisant partie de la géométrie de l’ordre. Le problème du zèbre est
bien connu.
Au moyen d’indices qui mettent en relation deux éléments ou
plus, il s’agit de reconstituer le tableau complet de façon à identifier le
propriétaire du zèbre. C’est généralement sous une forme semblable que se
présentent les récréations d’affectation. Des informations sont données
qui permettent de déduire que certains éléments sont liés ou tout à fait
sans relation. En combinant ensemble toutes les déductions, on en arrive à
replacer tous les éléments dans un contexte cohérent et vérifiable.
Problème 29.
Gabrielle, Sara et Rosalie demeurent dans trois quartiers différents :
Hochelaga, Mont-Royal et Ville-Marie.
1. La fille du
quartier Mont-Royal a téléphoné à Sara.
2. Rosalie et la
fille du quartier Ville-Marie ont déjeuné ensemble.
3. Sara aime bien
visiter les restaurants du quartier Ville-Marie qui est voisin du sien.
Déterminez le
quartier où habite chaque fille.
Les récréations de vérité
Une proposition est
vraie ou fausse. Voilà une proposition qui doit être vraie. Car, si elle
était fausse, une affirmation ne serait pas toujours vraie ou fausse. Et si
elle était ni fausse ni vraie, que serait-elle ? Il y a des gens qui
disent la vérité, d’autres qui mentent. C’est à partir de cette réalité
que des récréations ont été produites. On rencontre alors trois types de
personnes :
celle qui dit toujours la vérité,
celle qui ment toujours,
celle qui parfois dit la vérité, parfois ment.
On ne connaît pas
toujours la disposition d’esprit des personnes si bien que leurs paroles
peuvent demeurer ambiguës tant qu’on n’a pas trouvé les liens logiques qui
les unissent.
Problème 30.
Dans une salle, il y a 16 personnes. L’une d’elles a gagné un voyage
dans le Sud. À tour de rôle, chacune affirme qu’elle connaît le
gagnant. Une seule personne dit la vérité, tandis que les autres mentent.
|
01
Le gagnant
est 08 |
02
Le gagnant
est 07 |
03
Le gagnant
est 10 |
04
Le gagnant
est 15 |
|
05
Le gagnant
est 12 |
06
Le gagnant
est 15 |
07
Le gagnant
est 03 |
08
Le gagnant
est 15 |
|
09
Le gagnant
est 15 |
10
Le gagnant
est 04 |
11
Le gagnant
est 08 |
12
Le gagnant
est 03 |
|
13
Le gagnant
est 10 |
14
Le gagnant
est 07 |
15
Le gagnant
est 10 |
16
Le gagnant
est 12 |
Qui a gagné un
voyage dans le Sud ?
Les déplacements
Les solitaires
peuvent être associés aux récréations logiques. Le matériel est souvent
constitué de jetons qui peuvent être déplacés selon des règles définies.
Problème 31.
Sur la grille de gauche, Élise dépose six jetons : deux blancs, deux
noirs et deux rouges. Un jeton se déplace horizontalement, verticalement ou
obliquement en sautant par-dessus un autre.
|
B |
B |
|
|
|
|
|
|
|
|
N |
N |
|
|
|
|
|
|
|
|
R |
R |
|
|
® |
B |
B |
R |
R |
|
|
|
|
|
|
|
|
N |
N |
Déplacez les
jetons de façon à obtenir la grille de droite.
La récréation
ci-après est inspirée du taquin, ce solitaire
qui fut très populaire à la fin du 19e siècle. On y associe une
pièce du jeu d’échecs.
Problème 32.
Gabrielle prend 15 jetons et les numérote de 1 à 15. Elle les place dans
une grille 4 ´ 4 comme ci-après. Elle déplace
un à un les jetons sur une case libre en respectant la marche du cavalier
aux échecs.
|
1 |
11 |
3 |
6 |
|
5 |
13 |
9 |
2 |
|
15 |
10 |
4 |
12 |
|
|
14 |
8 |
7 |
Déplacez les
jetons pour que, à la fin, les nombres apparaissent dans leur ordre
naturel.
La loi de formation
Ces récréations
présentent des nombres, des symboles ou des lettres qui se succèdent d’après
une loi de formation inconnue. On les retrouve notamment dans les tests
destinés à mesurer le quotient intellectuel. La loi de formation ne peut s’appuyer
que sur un nombre suffisant de données. Il peut arriver qu’on trouve une loi
de formation imprévue.
Problème 33.
Inscrivez dans les cercles vides le nombre manquant.
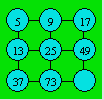
La loi de formation
ne fait pas toujours appel à des calculs. Celle-ci met par parfois à l’épreuve
la capacité visuelle.
Problème 34.
Dans ce tableau, les chiffres 0 et 1 ont été placés selon des
règles particulières. Complétez la dernière ligne du tableau.
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
La transposition de mots
Comme dans les
récréations cryptarithmiques, chaque lettre est représentée par un chiffre
différent. Pour chaque mot, on donne les chiffres dans le désordre. Par
exemple, les mots qui ont les mêmes lettres ont nécessairement les mêmes
chiffres.
Problème 35 .
Marc-Antoine choisit six lettres. Il écrit trois mots et indique les
chiffres pour chaque mot.
LIN : 273
BEL : 517 NEZ : 425
Quel est le
nombre qui correspond à BIEN ?
Les messages chiffrés
Cette forme de
récréations peut être résolue en se basant sur la grande fréquence de
certaines lettres comme le E, le S, le R et le T. On peut aussi analyser la fin
des mots où on trouve assez souvent une voyelle, principalement le E.
Problème 36.
On peut lire ci-dessous une phrase. À chaque nombre de 1 à 26 correspond
une lettre de l’alphabet. Quatre indices sont donnés.
|
10 |
21 |
|
7 |
19 |
18 |
18 |
21 |
|
21 |
2 |
9 |
|
13 |
3 |
21 |
|
11 |
22 |
5 |
13 |
18 |
21 |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
6 |
13 |
22 |
|
19 |
|
6 |
13 |
19 |
9 |
18 |
21 |
|
7 |
17 |
9 |
21 |
2 |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
C |
|
|
|
|
Déchiffrez cette
phrase.
Les carrés latins
Dans une grille, on
peut disposer des groupes d’objets différents de façon à ne jamais
retrouver le même objet plus d’une fois dans une même rangée. On a là le
domaine des carrés latins et gréco-latins.
Problème 37.
Dans une grille carrée 5 ´
5, placez les
lettres A, B, C, D, E, de façon à ne jamais retrouver la même lettre sur
toute ligne, colonne ou diagonale.
En guise de
conclusion.
Par ces
illustrations, on voit que les mathématiques récréatives touchent à des
sujets variés. Si on regarde autour de soi, on peut découvrir des situations
qui peuvent être traduites de façon à attirer et à divertir l’esprit
humain. La variété et la richesse des récréations mathématiques sont des
atouts qui peuvent leur permettre d’entrer à l’école. Elles peuvent servir
alors à développer le raisonnement mathématique et à augmenter la
performance en résolution de problèmes. Û
|
![]()
![]()