|
Hexagone
Polygone formé de six côtés.
L’hexagone régulier est l'objet de dissection. Il peut
être découpé en 12 ou 36 triangles rectangles congruents dans lesquels le
carré de la mesure du grand côté est égal au triple du carré de la mesure
du petit. De plus, il peut être découpé en un nombre minimum n de
pièces qui sont alors assemblées pour former chacune des figures indiquées.
Sauf les croix, les polygones sont réguliers.
Des hexagones réguliers congruents peuvent être assemblés
pour paver le plan. Pappus, un mathématicien grec du début du IVe
siècle, a démontré que l'hexagone régulier est, de tous les polygones qui
peuvent recouvrir le plan par juxtaposition, celui qui présente le périmètre
minimum pour une surface donnée. Un tel pavage peut recevoir des nombres
disposés selon des propriétés magiques.
Il y a 12 manières différentes de
joindre les sommets d'un hexagone de façon continue pour obtenir une courbe
fermée en passant une seule fois par chaque sommet. Voici un exemple de
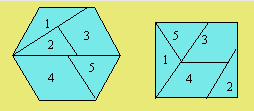
découpage d'un hexagone en cinq pièces qui, une fois assemblées, donnent un
carré :
Le tableau suivant contient les 10 plus petits nombres pour
chacune des classes de nombres figurés reliés à l’hexagone. La dimension D
est donnée pour chaque classe.
|
Classe |
D |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Gnomonique
|
1 |
1 |
5 |
9 |
13 |
17 |
21 |
25 |
29 |
33 |
37 |
|
Centré D1
|
1 |
1 |
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
|
Hexagonal
|
2 |
1 |
6 |
15 |
28 |
45 |
66 |
91 |
120 |
153 |
190 |
|
Centré
D2
|
2 |
1 |
7 |
19 |
37 |
61 |
91 |
127 |
169 |
217 |
271 |
|
Pyramidal
|
3 |
1 |
7 |
22 |
50 |
95 |
161 |
252 |
372 |
525 |
715 |
|
Centré
D3
|
3 |
1 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
729 |
1000 |
|
Hyperpyramidal
|
4 |
1 |
8 |
30 |
80 |
175 |
336 |
588 |
960 |
1485 |
2200 |
|
Centré
D4
|
4 |
1 |
9 |
36 |
100 |
225 |
441 |
784 |
1296 |
2025 |
3025 |
|
Pyramidal
D5
|
5 |
1 |
9 |
39 |
119 |
294 |
630 |
1218 |
2178 |
3663 |
5863 |
|
Centré
D5
|
5 |
1 |
10 |
46 |
146 |
371 |
812 |
1596 |
2892 |
4917 |
7942 |
|
Étoilé
|
2 |
1 |
12 |
33 |
64 |
105 |
156 |
217 |
288 |
369 |
460 |
|
Centré étoilé
|
2 |
1 |
13 |
37 |
73 |
121 |
181 |
253 |
337 |
433 |
541 |
L'hexagone peut être curviligne,
étoilé ou magique.
Il est parfois appelé alvéole à cause de sa forme.
© Charles-É. Jean
Index
: H
|
Voir aussi Hexagone dans
l'Aide-mémoire.
|
![]()
![]()