| Superposition
u
Faire une superposition.
– Stratégie de résolution de problème qui consiste à disposer l’un
au-dessus de l’autre des objets, des figures géométriques, des ensembles.
Les objets peuvent alors se confondre ou être transformés.
Cette stratégie en
est une d’enchaînement logique.
Problème 1. Dans cette figure, les segments AB et BC sont congruents. Il en
est de même des segments AD et DC. Montrez que le quadrilatère intérieur
occupe la moitié de la superficie du rectangle.
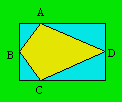
Démarche. On découpe le long des côtés du
quadrilatère intérieur et on superpose les parties dans la figure comme
ceci :
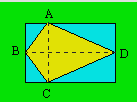
On pourrait vérifier aussi par pliage.
Problème 2. Dans une grille carrée 3 × 3,
placez les nombres : 11, 12, 13, 21, 22, 23, 31, 32 et 33. Sur chaque
rangée horizontale de même que sur chaque rangée verticale, on ne doit pas
trouver d’unité identique, ni de dizaine identique.
Démarche. On construit deux carrés latins, l’un avec les dizaines et l’autre
avec les unités. On superpose ces deux carrés.
|
2a |
1a |
3a |
|
3a |
1a |
2a |
|
23 |
11 |
32 |
|
3 |
2 |
1 |
|
1 |
2 |
3 |
= |
31 |
22 |
13 |
|
1 |
3 |
2 |
|
2 |
3 |
1 |
|
12 |
33 |
21 |
© Charles-É. Jean
Index
: S
|
Les stratégies d'enchaînement logique
mentionnées dans ce lexique sont :
1. Analyser les données
2. Composer un programme
3. Exclure les données superflues
4. Faire une fausse supposition
5. Faire une hypothèse
6. Faire plusieurs hypothèses
7. Faire une
observation raisonnée
8. Faire une superposition
9. Partir de l’unité
10. Prendre un raccourci
11. Prioriser des données
12. Procéder par analogie
13. Procéder par approximation
14. Procéder par bonds
15. Procéder par déduction
16. Procéder par élimination
17. Procéder par étapes concourantes
18. Procéder par induction
19. Procéder par itération
20. Procéder par progression
21. Procéder par régression
22.
Réduire à une seule condition
23. Résoudre un
problème auxiliaire
24.
Se donner des jalons
25. Simplifier les données
|
![]()
![]()