u Utiliser une proposition. – Stratégie de résolution de problèmes qui consiste à rechercher d'abord une proposition antérieurement démontrée et à l’utiliser pour résoudre le problème. Cette stratégie en est une d’application.

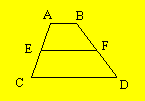
Problème 1. Dans ce trapèze, les segments AB et CD mesurent respectivement 15 et 27 centimètres. Les segments AE et EC sont congruents ; de même, BF et FD sont congruents. Trouvez la mesure du segment EF.

Démarche. Le segment EF mesure (15 + 27)/2, soit 21 centimètres. On a appliqué la proposition suivante : Dans un trapèze la droite qui joint les milieux des côtés non parallèles est égale à leur demi-somme.

Problème 2. Pauline dispose d'un coffre à neuf compartiments disposés en carrés dans le fond. Elle dispose ses timbres de telle façon que chaque compartiment reçoit 20, 21, 22, 23, 24, 25, 26, 27 ou 28 timbres. Elle a déjà posé 27 et 20 timbres dans les compartiments appropriés. 

Disposez les autres timbres pour qu'il y ait le même nombre de timbres sur chacune des huit rangées de trois compartiments.

Démarche. On commence par calculer le nombre total de timbres. Il y en a 216. Le problème est grandement simplifié si on connaît deux propositions.

1. Dans un carré magique d'ordre 3, la densité ou somme sur chaque rangée est égale au tiers de la somme totale.

2. Dans un carré magique d'ordre 3, le médian ou case du milieu contient un nombre qui est le tiers de la densité.

Selon la proposition 1, le nombre de timbres sur chaque rangée doit être de 216/3 ou 72. Selon la proposition 2, il y a 72/3 ou 24 timbres au milieu. Il ne reste maintenant qu'à inscrire 24 et à compléter par des calculs adéquats. La disposition des nombres est :

© Charles-É. Jean

Index : P