Géométriques

u Appliquer les propriétés des transformations géométriques. – Stratégie de résolution de problèmes qui consiste à rechercher d'abord les propriétés des transformations géométriques et à les utiliser pour résoudre le problème. Cette stratégie en est une d’application.

Problème 1. Combien y a-t-il de carrés magiques composés des mêmes nombres que celui illustré, mais dont au moins un nombre est dans une position différente ?

Démarche. En faisant faire une rotation au carré, les nombres changent de position mais la propriété magique du carré demeure invariante. On peut ainsi trouver trois carrés magiques.

Le premier carré magique est formé par une rotation de 90 degrés dans le sens anti-horaire à partir du carré donné. Chaque autre carré est formé à partir du précédent toujours à la suite d'une rotation. Pour trouver les quatre autres, on peut appliquer une symétrie sur chacun des carrés précédents, y compris le carré magique donné. L'axe de symétrie est la rangée horizontale du centre. On obtient ceci :

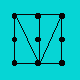
Problème 2. Dans le treillis suivant, les points sont les sommets de carrés unitaires.

Joignez les points par des segments de droites. Combien pouvez-vous construire de triangles rectangles non isocèles ?

Démarche. On obtient quatre triangles comme ci-dessous. Puis, on fait successivement une rotation de 90 degrés : ce qui donne 12 autres triangles. Il y a en tout 16 triangles qui répondent aux conditions.

© Charles-É. Jean

Index : G